Основные методы решения задач моделирования

На этапе программной реализации модели и реализации плана экспери­ментов необходим выбор методов решения задач моделирования. При этом используются три основные группы методов:

1) графические — оценочные приближенные методы, основанные на по­строении и анализе графиков;

2)аналитические — решения, полученные строго в виде аналитических выражений (пригодны для узкого круга задач);

3) численные — основной инструмент для решения сложных математических задач, основанный на применении различных численных методов, современных прикладных программ, средств визуализации и анализа получаемых результатов.

Аналитическое решение удается получить редко и чаще всего лишь при упрощенной формулировке задачи моделирования в линейном приближении. Основным средством моделирования является алгоритмический подход, реа­лизующий вычислительный эксперимент на персо­нальном компьютере. Получаемое на ЭВМ решение почти всегда содер­жит некоторую погрешность. Абсолютная погрешность

есть разность между приближенным 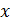и точным или идеальным х_и значения­ми результата, а относительная погрешность определяется как

Наличие погрешности решения обусловлено рядом причин. Перечислим основные источники погрешности.

1. Математическая модель является лишь приближенным описанием реа­льного процесса (погрешность модели).

2. Исходные данные, как правило, содержат погрешности, поскольку яв­ляются результатами приближенных экспериментов (измерений) или решени­ями вспомогательных задач (погрешность данных).

3. Применяемые для решения задачи методы в большинстве случаев явля­ются приближенными (погрешность метода).

4. При вводе исходных данных в компьютер, выполнении им операций произво­дятся округления (вычислительная погрешность).

Погрешности, указанные в пунктах 1 и 2 — неустранимые на данном этапе решения, для их уменьшения приходится возвращаться вновь к построению математической, а иногда и концептуальной модели, проводить дополнительное эксперимен­тальное уточнение условий задачи.

Оценка обусловленности вычислительной задачи — еще одно обязательное требование при выборе метода решения и построении математической модели.

Пусть вычислительная задача корректна. Теоретически устойчивость зада­чи означает, что ее решение может быть найдено со сколь угодно малой по­грешностью, если гарантируется достаточно малая погрешность входных данных. Однако на практике их точность ограничена (и величиной гораздо большей, чем - машинная точность, р – разрядность компьютера, при этом округление производится усечением числа).

Как влияют малые, но конечные погрешности входных данных на реше­ние? Насколько сильно они искажают результат? Ответ на это дает понятие обусловленности задачи, т. е. чувствительности решения вычислительной задачи к малым погрешностям входных данных.

Задачу называют хорошо обусловленной, если малым погрешностям входных данных отвечают малые погрешности решения, и плохо обусловленной, если возможны сильные изменения решения. Часто возможно ввести количественную оценку степени обусловленности - число обусловленности. Его можно интерпретировать как коэффициент возможного возрастания погрешности в решении по отношению к вызвавшей их погрешности входных данных. Если установлено неравенство между этими погрешностями, то можно пользоваться следующими выражениями:

и

где ν_Δ - абсолютное число обусловленности ν_δ — относительное число обу­словленности. Для плохо обусловленных задач , неустойчивость соответ­ствует .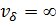

При каких значениях можно считать задачу плохо обусловленной? Это зависит от требований к точности решения и от уровня обеспечиваемой точ­ности исходных данных.

Если требуется найти решение с точностью 0.1 %, а входная информация задается с точностью в 0.02%, то при ν_δ= 10 уже будет плохая обусловлен­ность.

Однако если исходные данные задаются с δ(x*) < 0.0001 %, то при ν_δ= 10³ - задача хорошо обусловлена (δ (у*) = 0.1 %).

Вычислительные методы, как правило, преобразуются к виду, удобному для програм­мной реализации. Можно выделить следующие классы численных методов:

• Метод эквивалентных преобразований - исходную задачу заменяют другой, имеющей то же решение: нахождение корня нелинейного уравне­ния f(x) = 0 сводят к поиску точек глобального минимума Ф(х) = (f(х))².

• Методы аппроксимации - заменяют исходную задачу другой, решение которой близко к решению исходной задачи.

• Методы конечно-разностные - основанные на замене производных конечными разностями, например

• Прямые (точные) методы - решение может быть получено за конечное число элементарных операций (арифметические и извлечение корня). Многие прямые методы не годятся к применению в ЭВМ из-за чувстви­тельности к ошибкам округления.

• Итерационные методы - методы последовательных приближений к ре­шению задачи. Задается начальное приближение решения, строится итерационная последовательность приближений к решению. Если эта последовательность сходится к решению, то говорят что итерационный процесс сходится. Множество начальных приближений, для которых метод сходится, называются областью сходимости метода.

• Методы статистических испытаний (Монте-Карло) - основаны на мо­делировании случайных величин и построении статистических оценок решений задач (для моделирования больших систем). Для реализации этих методов используются генераторы случайных чисел.

Численные методы группируются вокруг типичных математических задач: задач анализа, алгебры, оптимизации, решения дифференциальных и интег­ральных уравнений, обратных задач (синтез). Этот этап решения заканчивает­ся выбором и обоснованием конкретных численных методов решения, разра­боткой алгоритма, которые могут быть программно реализованы средствами компьютерной техники.