Методика определения критериев подобия на основе анализа размерностей

Данная методика является универсальной, что позволяет путем определенной последовательности действий найти безразмерные комбинации, которые характеризуют рассматриваемый технический объект, не зависимо от его физической природы. Решение этой задачи состоит из трех этапов.

На первомэтапе выбираются фундаментальные переменные. Обычно при выборе выходной переменной осложнений не бывает. Как правило, заранее известно, что необходимо определить. Входной фундаментальной переменной (фактором), как отмечалось ранее, является любая величина, влияющая на отклик, и способная изменяться независимо от других. Для правильного выбора фундаментальных переменных необходимо глубокое понимание сути исследуемого объекта. Часто это требует не только изучения априорной информации, но и постановки предварительных экспериментов. Если после выбора фундаментальных переменных система безразмерных комбинаций не получается, то необходимо возвратиться к анализу объекта исследования.

На втором этапе выбирается система основных единиц для выражения размерностей фундаментальных переменных. В качестве основных ре­комендуется принимать основные единицы СИ:

метр - единица длины l , размерность L ;

килограмм - единица массы m , размерность М ;

секунда - единица времени t , размерность Т;

ампер - единица силы электрического тока i, размерность I;

кельвин - единица термодинамической температуры Ө, размерность К;

моль - единица количества вещества n , размерность N;

кандела - единица силы света j, размерность J.

Используя размерности основных единиц, можно составить формулы размерностей всех фундаментальных переменных. Например, известно, что сила определяется зависимостью .

Формула размерности силы определяется как произведение формул размерности массы и ускорения

Записав формулы размерностей всех фундаментальных переменных, описывающих процессы в объекте, устанавливают, какие размерности основных единиц в них входят. Эти единицы и будут составлять систему основных единиц в условиях конкретной задачи.

На третьем, заключительном этапе определяются критерии подобия с использованием теории размерностей.

Для уяснения способа нахождения безразмерных критериев с помощью теории размерности рассмотрим пример решения задачи.

Пример решения задачи по определению критериев подобия процесса силового взаимодействия шара с обтекающим потоком жидкости.

Схема стенда для определения силы, с которой поток действует на шар, показана на рис.2.1. Шар помещен в трубопровод настолько большого внутреннего диаметра, что стеснением им потока можно пренебречь. Гибкой нитью шар связан через блок с пружинным динамометром. Усилие зависит от свойств шара и потока. Если шероховатостью шара можно пренебречь (шар выполнен гладким), то его свойства определяются одной переменной - диаметром . Свойства потока оцениваются средней скоростью , плотностью 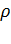и вязкостью жидкости. Таким образом, в рассматриваемом случае фундаментальных переменных пять: выходной параметр и факторы .

Для выбора основных единиц запишем формулы размерностей фундаментальных переменных. Наименования фундаментальных переменных, их обозначения и размерности приведены в табл.2.2. Из данных, приведенных в таблице, следует, что размерности всех фундаментальных переменных можно выразить тремя основными единицами – . Так как число фундаментльных переменных в этой задаче равно пяти, а число основных единиц – три, то независимых критериев будет

Таблица 2.2

Наименования, обозначения и размерности фундаментальных переменных

Фундаментальные переменные	Обозначение	Размерность
Сила
Скорость
Плотность жидкости
Вязкость динамическая
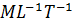
Диаметр шара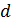

Рис.2.1. Схема стенда для определения силы воздействия потока на шар

Критерий - безразмерная комбинация - в общем случае может быть представлена произведением фундаментальных переменных в определенных степенях. В рассматриваемом случае критерий где - показатели степеней. Показатели могут быть целыми, дробными, положительными и отрицательными числами. Они могут принимать и нулевое значение. В последнем случае критерий не будет зависеть от соответствующей фундаментальной переменной.

Будем искать произведение критериев и в виде

(2.7)

где - неизвестные показатели степеней.

Если зависимость (2.7) справедлива относительно переменных, то она будет справедлива и относительно размерностей. Подставим в (2.7) вместо переменных их размерности. При этом будем учитывать, что поскольку критерии безразмерны, то левая часть уравнения представлена произведением размерностей в нулевых степенях:

Чтобы последнее выражение было справедливым, должны выполняться условия:

для 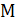, (2.8)

для (2.9)

для (2.10)

В трех уравнениях пять переменных. Решив совместно уравнения (2.8) – (2.10), можно исключить три переменные. От того, какие переменные исключаются, зависит вид критериев. Все критерии будут формально верными. Однако одни из них имеют ясный физический смысл, а другие - нет. Поэтому решение задачи по установлению вида критериев иногда приходится повторять при различных комбинациях исключаемых переменных. Выразим переменные 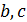и через и .

Из выражений (2.8) и (2.9) получим

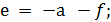(2.11)

. (2.12)

После подстановки в зависимость (2.10) значения степени из (2.11) и степени из (2.12) имеем

(2.13)

Подставим в выражение (2.7) показатели степеней и :

.

Объединим члены последнего уравнения, имеющие одинаковые по­казатели степеней:

Из последнего выражения следует, что в качестве критериев подобия могут быть приняты комплексы 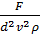и . Первый является безразмерным усилием. Усилие, действующее со стороны потока на шар, делится на . Здесь - площадь квадрата, сторона которого равна диаметру шара; - удвоенное скоростное давление. Так как кинематический коэффициент вязкости жидкости 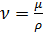, а , то критерий . По теории подобия произведение, частное нескольких критериев или возведение их в произвольную степень дают новый критерий. Таких критериев можно получить бесчисленное множество. Однако независимых среди них будет только критериев.

При установлении зависимости силы от определяющих факторов без перехода к безразмерным комбинациям необходимо фиксировать диаметр, скорость, плотность и вязкость на определенном числе уровней, например на пяти. Для плотности и вязкости независимость изменения при этом практически реализовать нельзя. После перехода к безразмерным комбинациям при постановке эксперимента необходимо изменять только одну из входных величин. Проще всего изменению поддается скорость. Установив, пять уровней скорости, получим пять соответствующих уровней числа Рейнольдса. Диаметр шара, вязкость и плотность будут оставаться неизменными в течение всего исследования.