
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уровни детализации математических моделей
Когда проводятся исследования по разработке имитационной модели реальной системы, невозможно моделировать сразу всю систему в целом. Так, в САПР принято разделение математических моделей по уровням их детализации. Такой подход позволяет структуро представить себе области применения различных видов моделей и систематизировать их путем иерархической классификации. Вначале моделируются подсистемы, которые имеют отношение к исследуемой проблеме. Они включают части системы на различных уровнях детализации. Графически это можно представить в виде пирамиды управления (рис. 1.4). Набор выделенных областей формирует те части системы, которые включены в модель.
| Метауровень |
| Макроуровень |
| Микроуровень |
| Исследуемая проблема |
Рисунок 1.4 - Пирамида уровней детализации математических моделей
На любом уровне объект исследования представляют в виде некоторой системы, состоящей из элементов. В этой связи различают математические модели элементов и систем.
Всякая система – это сложный объект, который не может быть сведен просто к совокупности всех своих частей благодаря наличию связей, объединяющих различные части в одно целое. Причем отдельные части могут быть связаны друг с другом элементами - посредниками. Следовательно, поведение некоторых частей системы может приобретать новое качество, которого нет у ее элементов. В целом система может повести себя иначе, чем предсказывалось на основе анализа свойств ее элементов. Такое свойство системы называется эмерджентностьюили более известным словосочетанием «системный эффект».По мере усложнения систем не увидеть системный эффект обходится очень дорого.
При переходе к более высокому уровню система низшего уровня становится элементом нового уровня и, наоборот, при переходе к низшему уровню элемент становится системой. Обычно, чем ниже уровень, тем более детально описание его физических свойств. Следовательно, на низших уровнях используют наиболее сложные математические модели. На высших уровнях могут быть применены более простые модели.
В зависимости от степени абстрагирования при описании физических свойств технической системы различают три основных технических уровня (рис. 1.4): верхний или метауровень; средний или макроуровень; нижний или микроуровень.
Метауровеньсоответствует начальные стадиям проектирования, задачей которого является научно-технический поиск и прогнозирование, разработка концепции и технического решения, разработка технического предложения. Обычно на этом уровне используются методы теории графов, математической логики, теории автоматического управления, теории массового обслуживания, теории конечных автоматов.
Например, задачу по созданию автоматизации производственного участка с использованием пневмоавтоматики можно представить в виде графа, отображающего работу исполнительных механизмов (рис.1.5.). Такое представление позволяет проанализировать работу системы, и, если необходимо, дополнить ее специальными элементами памяти, которые обеспечат надежное выполнение рабочего цикла.

Риунок 1.5 – Граф-схема системы гидро- или пневмоавтоматики
На макроуровне объект рассматривается как динамическая система с сосредоточенными параметрами. Математические модели этого уровня обычно представляют собой системы обыкновенных дифференциальных уравнений. Эти модели используются обычно для определения параметров технического объекта и его функциональных элементов. Так, задача, представленная ранее с помощью граф-схемы, на макроуровне рассмтривается в виде принципиальной схемы (рис.1.6), описываемой системой обыкновенных дифференциальных уравнений.
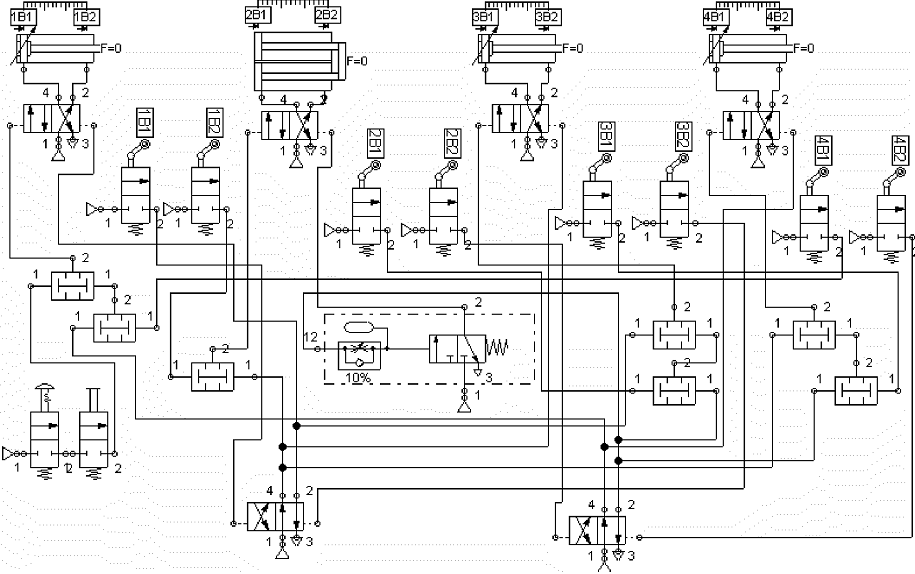
Рисунок 1.6 - Пример принципиальная схема пневмоавтоматики
Уравнения, описывающие движение поршней пневмоцилиндров, и изменения давления в рабочих камерах имеют вид:

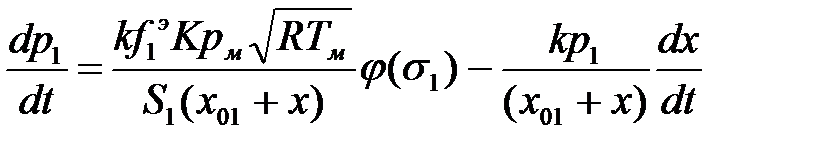


Решение такой системы дифференциальных уравнений, как правило, ищется с помощью численных методов Рунге-Кута, реализованных в прикладных пакетах MathCad, Matlab и т.п.
На микроуровне объект представляется как сплошная среда с распределенными параметрами. Для математического описания процессов функционирования обычно используются дифференциальные уравнения в частных производных. На микроуровне проектируются неделимые по функциональному признаку элементы, которые называются базовыми.
Основными уравнениями математической физики являются:
Ø Уравнения механических колебаний струн, стержней, мембран и трехмерных объектов (волновые уравнения), электромагнихных колебаний приводятся к виду: 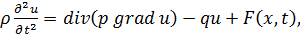 где неизвестная функция
где неизвестная функция 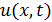 зависит, в общем случае от
зависит, в общем случае от 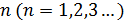 пространственных координат
пространственных координат 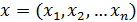 и времени
и времени 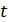 ; коэффициенты
; коэффициенты  определяются свойствами среды, где происходит колебательный процесс;
определяются свойствами среды, где происходит колебательный процесс; 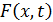 - выражает интенсивность внешнего возмущения. По определению операторов дивергенции
- выражает интенсивность внешнего возмущения. По определению операторов дивергенции 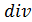 и градиента
и градиента 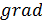
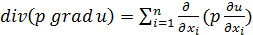
Ø Уравнение диффузии описывает процессы распространения тепла или диффузии частиц в среде: 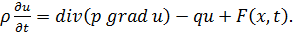
Ø Стационарные уравнения описывают стационарные процессы, для которых  и
и 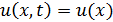 , при этом и уравнение колебаний, и уравнение диффузии примут вид:
, при этом и уравнение колебаний, и уравнение диффузии примут вид: 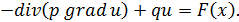 При
При 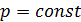 и
и 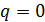 стационарное уравнение называется уравнением Пуассона и записывается
стационарное уравнение называется уравнением Пуассона и записывается  При
При  уравнение Пуассона называется уравнением Лапласа
уравнение Пуассона называется уравнением Лапласа 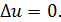
Ø Уравнения гидродинамики описываются системой следующих уравнений: 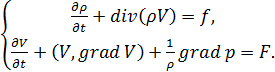 Это, соответственно, уравнение неразрывности потока и уравнение движения Эйлера. Чтобы замкнуть эту систему необходимо добавить уравнение состояния, задающее связь между давлением и плотностью:
Это, соответственно, уравнение неразрывности потока и уравнение движения Эйлера. Чтобы замкнуть эту систему необходимо добавить уравнение состояния, задающее связь между давлением и плотностью: 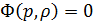 .
.
Из курса математической физики [] известно, что путем приведения уравнений в частных производных к каноническому виду, можно определить его тип, который может быть эллиптическим, параболическим, гиперболическим или смешанным.Так, уравнение Лапласа относится к эллиптическому типу, уравнение теплопроводности – параболического типа, а волновые уравнения являются гиперболическими.
На рис.1.7 показана структура нахождения решения для математической модели, соответствующей каждому из уровней детализации задачи.
| Микроуровень |
| Макроуровень |
| Метауровень |
| ДУЧП |
| ОДУ |
| Специфические модели |
| САУ |
| СЛАУ |
| Элементарные арифметические операции |
Рисунок 1.7 - Процесс нахождения решений математических моделей различных уровней
В приведенной структурной схеме приняты общеизвестные сокращения:
ДУЧП - дифференциальные уравнения с частными производными;
ОДУ - обыкновенные дифференциальные уравнения;
САУ – системы алгебраических уравнения;
СЛАУ - системы линейных алгебраических уравнений.
Стрелками показаны пути дискретизации моделей, т.е. их преобразование, необходимое для нахождения решения.
Первой ветви соответствует постановка задачи, относящейся к микроуровню, как краевой, чаще всего в виде дифференциальных уравнений в частных производных. Их численные методы решения основаны на дискретизации переменных и алгебраизации задачи. То есть от частных производных исследователь переходит к решению системы алгебраических уравнений путем представления исходных уравнений в виде разностной схемы, где производные заменяются конечными разностями. Другими словами, дискретизация - это замена непрерывных переменных конечным множеством их значений в заданных для исследования пространственном и временном интервалах; алгебраизация - замена алгебраическими соотношениями.
Дата добавления: 2014-11-13; просмотров: 439; Мы поможем в написании вашей работы!; Нарушение авторских прав |