
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Активные с программным управлением,
Активные с обратной связью,
Активно-пассивные эксперименты.
Пассивный экспериментоснован на регистрации входных и выходных параметров, характеризующих объект исследования без вмешательства в ход эксперимента. Обработка собранных экспериментальных данных осуществляется после окончания эксперимента. Обычно изменяется только один фактор при фиксированных значениях всех остальных.
При активномэксперименте предполагается возможность активного воздействия на объект исследования. Т.е. на вход объекта подаются возмущающие воздействия, на выходе регистрируются статические и динамические характеристики. При активном эксперименте можно оценить дисперсию ошибки, строго проверить адекватность модели, выполнить множественный регрессионный анализ.
Активный эксперимент с программой управления проводится по заранее составленному плану. В соответствии с этим планом осуществляется воздействие экспериментатора на входные параметры и регистрируются выходные, что позволяет выяснить природу происходящих в объекте процессов.
В случае активного эксперимента с обратной связью, имея результаты эксперимента на каждом шаге, можно выбрать оптимальную стратегию управления экспериментом. Такие эксперименты можно проводить автоматически.
Активно-пассивныйэксперимент характеризуется тем, что при его проведении одна часть данных регистрируется, а другая просто фиксируется и обрабатывается в процессе эксперимента. В таком эксперименте имеется два вида характеристик: одна часть – изменяющиеся под воздействием управляющих сигналов, вторая - не подверженные управляющим воздействиям.
Если эксперимент хорошо продуман и удачно спланирован, то он имеет больше шансов на успех. Основываясь на известных теориях и экспериментальных результатах, можно так выбрать способы и методы измерений, чтобы получить как можно больше сведений. Очень важно исключить влияние внешней среды или свести его к нулю.
Основные понятия математического планирования эксперимента
Под планированием эксперимента принято понимать:
· Раздел математической статистики, изучающий рациональную организацию измерений, подверженных случайным ошибкам;
· Процедуру выбора числа условий проведения опытов, необходимых и достаточных для решения поставленных задач с заданной точностью.
Важнейшими задачами методов обработки полученной в ходе эксперимента информации являются:
во-первых, задача построения математической модели изучаемого явления, процесса, объекта. Ее можно использовать и при анализе процессов и при проектировании объектов. Можно получить хорошо аппроксимирующую математическую модель, если целенаправленно применяется активный эксперимент;
во-вторых, задача оптимизации, т.е. нахождения такой комбинации входных независимых переменных, при которой выбранный показатель оптимальности принимает экстремальное значение.
План эксперимента – совокупность данных, определяющих число, условия и порядок проведения опытов.
Планирование эксперимента – выбор плана эксперимента, удовлетворяющего заданным требованиям, совокупность действий направленных на разработку стратегии экспериментирования (от получения априорной информации до получения работоспособной математической модели или определения оптимальных условий). Это целенаправленное управление экспериментом, реализуемое в условиях неполного знания механизма изучаемого явления.
В процессе измерений, обработки полученных данных, формализации результатов в виде математической модели, возникают погрешности, и теряется часть информации, содержащейся в исходных данных. Применение методов планирования эксперимента позволяет определить погрешность математической модели и судить об адекватности полученной модели. Если точность модели оказывается недостаточной, то применение методов планирования эксперимента позволяет модернизировать математическую модель с проведением дополнительных опытов без потери предыдущей информации и с минимальными затратами.
Цель планирования эксперимента – нахождение таких условий и правил проведения опытов, при которых удается получить надежную и достоверную информацию об объекте с наименьшей затратой труда, а также представить эту информацию в компактной и удобной форме с количественной оценкой точности.
Итак, планирование эксперимента предполагает, что эксперимент является активным и объект исследования представлен в виде модели «черный ящик». При этом используются только группа входных контролируемых параметров  ,называемых факторами, и один параметр
,называемых факторами, и один параметр  из группы выходных параметров
из группы выходных параметров  . Совокупность факторов образует факторное пространство, а зависимая переменная
. Совокупность факторов образует факторное пространство, а зависимая переменная 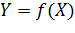 , которую требуется оптимизировать по какому-либо критерию, называется функций отклика. Геометрическое представление функции отклика в
, которую требуется оптимизировать по какому-либо критерию, называется функций отклика. Геометрическое представление функции отклика в  -мерном факторном пространстве образует поверхность отклика.
-мерном факторном пространстве образует поверхность отклика.
При выборе диапазонов изменения факторов нужно учитывать их совместимость, т.е. контролировать, чтобы в этих диапазонах любые сочетания факторов были бы реализуемы в опытах и не приводили бы к абсурду. Для каждого из факторов указывают граничные значения

Регрессионный анализ функции отклика предназначен для получения ее математической модели в виде уравнения регрессии

где В1, …, Вm – некоторые коэффициенты; е – погрешность.
Типовой задачей экспериментального исследования технической системы является необходимость оптимизировать функцию отклика, описание которой неизвестно. Обычно уравнение объекта ищется в виде полинома вида
 (3.1)
(3.1)
где  - коэффициенты регрессии. При этом целью планирования эксперимента является отыскание оценок коэффициентов уравнения модели (3.1) по результатам опытов в
- коэффициенты регрессии. При этом целью планирования эксперимента является отыскание оценок коэффициентов уравнения модели (3.1) по результатам опытов в 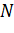 точках факторного пространства.
точках факторного пространства.
Среди основных методов планирования, применяемых на разных этапах исследования, используют:
· планирование отсеивающего эксперимента, основное значение которого выделение из всей совокупности факторов группы существенных факторов, подлежащих дальнейшему детальному изучению;
· планирование эксперимента для дисперсионного анализа, т.е. составление планов для объектов с качественными факторами;
· планирование регрессионного эксперимента, позволяющего получать регрессионные модели (полиномиальные и иные);
· планирование экстремального эксперимента, в котором главная задача – экспериментальная оптимизация объекта исследования;
· планирование при изучении динамических процессов и т.д.
Инициатором применения планирования эксперимента является Рональд А. Фишер, другой автор известных первых работ – Френк Йетс. Далее идеи планирования эксперимента формировались в трудах Дж. Бокса, Дж. Кифера. В нашей стране - в трудах Г.К. Круга, Е.В. Маркова и др.
В настоящее время методы планирования эксперимента заложены в специализированных пакетах программных продуктов, например: StatGrapfics, Statistica, SPSS, SYSTAT и др.
При использовании методов планирования эксперимента необходимо найти ответы на 4 вопроса:
· Какие сочетания факторов и сколько таких сочетаний необходимо взять для определения функции отклика?
· Как найти коэффициенты  ?
?
· Как оценить точность представления функции отклика?
· Как использовать полученное представление для поиска оптимальных значений  ?
?
Геометрическое представление функции отклика в факторном пространстве  в виде поверхности отклика показано на рис. 3.1 .
в виде поверхности отклика показано на рис. 3.1 .
При трех и более факторах задача становится достаточно сложной, при ее решении путем простого перебора всех факторов. Если и будут найдены решения, то использовать совокупность выражений достаточно трудно, а часто и не реально.
| X1 |
| X2 |
| Y=F(X) |
Рисунок 3.1- Графическое изображение поверхность отклика
Например, пусть необходимо исследовать влияние скорости  , плотности
, плотности  движущейся жидкости и внутреннего диаметра трубопровода
движущейся жидкости и внутреннего диаметра трубопровода 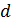 на потери давления
на потери давления  и расход жидкости
и расход жидкости  при проектировании гидравлической сети (рис. 3.2).
при проектировании гидравлической сети (рис. 3.2).

|

|
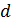
|
| Объект исследования – трубопровод |

|

|
Рисунок 3.2 – Пример постановки задачи исследования влияния факторов на отклики
Если в диапазоне изменения каждого фактора взять хотя бы по шесть точек, см.табл.3.1, то для того чтобы выполнить опыты при всех возможных сочетаниях значений факторов (их три) необходимо выполнить 63=216 опытов и сформировать по 62=36 кривых для каждой из двух функций отклика.
Таблица 3.1
Значения факторов для проведения эксперимента
| Факторы | Размер- ности | ||||||

| м/с | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |

| кг/м3 | ||||||
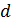
| м | 0,05 | 0,075 | 0,1 | 0,125 | 0,15 | 0,175 |
Если же необходимо продублировать опыты, чтобы снизить погрешность, то число опытов пропорционально возрастает, поэтому произвольное выполнение опытов при числе факторов более двух и использование их результатов - практически нереально.
Дата добавления: 2014-11-13; просмотров: 1640; Мы поможем в написании вашей работы!; Нарушение авторских прав |