Метод крутого восхождения

Известно, что кратчайший путь – это движение по градиенту, т.е. перпендикулярно касательным к линиям уровня, на которых функция отклика принимает постоянные значения

В связи с этим при оптимизации рабочее движение целесообразно совмещать в направлении наиболее быстрого возрастания функции отклика, т.е. в направлении градиента функции. Как известно, градиентом функции называется вектор , направленный из данной точки по нормали к касательной проходящей через нее кривой или поверхности равного уровня в сторону наискорейшего возрастания указанной функции. Существует несколько модификаций градиентного метода, одним из них является метод крутого восхождения. Сущность его отражена на рис.3.6.

В этом случае шаговое движение осуществляется в направлении наискорейшего возрастания функции отклика, т.е 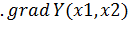. Однако направление корректируется не после следующего шага, а при достижении в некоторой точке на данном направлении частного экстремума функции отклика.

Рисунок 3.6 - Процедура оптимизации методом крутого восхождения

Пусть в окрестности точки М_о, как центра плана, поставлен ПФЭ 2². Координаты отдельных опытов соответствуют точкам 1-4. По результатам ПФЭ можно рассчитать коэффициенты линейного уравнения регрессии:

(3.9)

После чего можно найти градиент

,

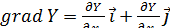продифференцировав уравнение (3.9):

Для движения по градиенту необходимо изменять факторы пропорционально их коэффициентам регрессии в сторону, соответствующую знакам коэффициентов. В процессе поиска двигаются в этом направлении, пока не будет найден локальный максимум (т.М₁). после чего находят направление градиента, осуществляя ПФЭ, и далее процедура повторяется.

Практически алгоритм сводится к следующей последовательности операций:

1. Планирование и постановка ПФЭ (или ДФЭ) в окрестности точки начального состояния (М₀). Расчет коэффициентов линейной регрессии; определении направления градиента.

2. Расчет произведений где - интервал варьирования факторов при ПФЭ (ДФЭ).

3. Выбор базового фактора , у которого

4. Выбор шага крутого восхождения для базового фактора производится на базе априорной информации и опыта исследователя. Следует учесть, что слишком малый шаг потребует значительного числа опытов, а большой – создает опасность проскакивания области оптимума.

5. Расчет шагов изменения других факторов по формуле: . Это соотношение между величинами шагов изменения отдельных факторов обеспечивает движение по градиенту в факторном пространстве.

6. Составление плана движения по градиенту: в соответствии с определенными значениями шагов изменения факторов Находят координаты опытов 5,6,7. Часть этих опытов проводят «мысленно». «Мысленный» опыт заключается в получении предсказанных (расчетных) значений функции отклика по линейному уравнению регрессии, что позволяет сократить объем реальных опытов. Обычно реальные опыты ставят через 3-4 «мысленных» для того, чтобы подтвердить действительное возрастание отклика. Из опытных данных находят положение локального экстремума.

7. В окрестности локального экстремума ставят новую серию опытов (ПФЭ или ДФЭ) для определения новых значений коэффициентов уравнения регрессии и нового направления градиента. В дальнейшем процедура повторяется до достижения нового локального экстремума и т.д., вплоть до определения окрестности координат максимума функции отклика, которая носит название почти стационарной области.

Признаком достижения этой области является статистическая незначимость коэффициентов . В этой области становятся значимыми эффекты взаимодействия и квадратичные эффекты. Здесь требуется переходить от ДФЭ к ПФЭ и к планам второго порядка.

Для задач, где требуется определить координаты не максимума, а минимума функции отклика, знаки следует поменять на обратные. Движение будет происходить в направлении, обратном вектору градиента.

Симплекс-планирование

Позволяет без предварительного изучения влияния факторов найти область оптимума. Т.к. здесь не требуется определение градиента, то этот метод относится безградиентным метода поиска оптимума. Для этого используется специальный план эксперимента в виде симплекса.

Симплекс – простейший выпуклый многогранник, образованный вершинами в -мерном пространстве, которые соединены между собой прямыми линиями. При этом координаты вершин симплекса являются значениями факторов в отдельных опытах.

, симплекс- треугольник, – тетраэдр и т.д.

Симплекс называется правильным, если все расстояния между его вершинами (ребра) равны.

Алгоритм симплекс планирования:

Строится исходный симплекс, проводятся опыты в его вершинах и анализируются результаты.

1. Выбирается вершина, в которой получено наименьшее значение функции отклика. Для движения к оптимуму ставится опыт в новой точке, являющейся зеркальным отображением точки с наихудшим (минимальным) результатом. Процесс повторяется до тех пор, пока не будет найдена почти стационарная область.

2. Не смотря на то, что путь может быть и не прямолинеен, общее число опытов может быть не большим.

При симплекс-планировании выбор размеров симплекса и его начальное положение произволен.

Для окончания процесса используются следующие критерии:

1 – разность значений функции отклика в вершинах симплекса становится меньше ранее заданной. Это означает вход в почти стационарную область вблизи оптимума, либо достижения области оптимума в виде «плато»;

2 - отражение любой из вершин симплекса после однократного «качания» приводит к возврату в исходное положение. При этом есть основания считать, что симплекс накрыл область оптимума.

3 – циклическое движение симплекса вокруг одной из его вершин на протяжении более, чем нескольких шагов. Т.е. циркулирует вокруг области оптимума.

В случаях 2 и 3 рекомендуется уменьшать размеры симплекса, т.е. расстояние между вершинами, до уточнения координаты оптимума.

Данный метод прост, но работает не достаточно быстро. Наиболее быстрым является метод, основанный на его модификации - метод деформируемого многогранника.

Ускорение достигается за счет того, что отражение осуществляется не на постоянную величину.

На рис. 3.7 показана точка 4 очередного опыта при нормальном отражении наихудшей вершины 1, точки 5′, 5′′, 5′′′ последующих опытов для случаев, соответственно, растяжения, сжатия и отрицательного сжатия многогранника.