КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Полный и дробный факторные эксперименты
Эксперимент, в котором реализуются все возможные сочетания уровней факторов, называют полным факторным экспериментом (ПФЭ). При двух уровнях имеем ПФЭ типа 
. Число опытов для данного случая будет равно
Условие эксперимента записываются в виде таблицы. Строки её соответствуют различным опытам (вектор-строка), столбцы - значениям факторов в кодированном виде (вектор-столбцы). Такие таблицы называются матрицами планирования эксперимента (МПЭ).
Составим МПЭ для двумерной модели на двух уровнях 
(табл.3.2). Число опытов = 4.
Таблица 3.2
Матрица планирования ПФЭ
| Номер опыта | 
| 
| 
|
| -1 | -1 | y1 | |
| +1 | -1 | y2 | |
| -1 | +1 | y3 | |
| +1 | +1 | y4 |
Для плана каждая комбинация факторов представляет собой вершину квадрата. Поэтому такое планирование называют ортогональным. Данная матрица обладает рядом свойств, которые определяют качество модели, т.е. делают оценки коэффициентов модели наилучшими. Первые два свойства вытекают из построения матрицы.
Симметричность относительно центра эксперимента. Алгебраическая сумма элементов столбца каждого фактора равно нулю:
, где 
- номер фактора, 
- число опытов.
Условие нормировки. Сумма квадратов элементов каждого столбца равна числу опытов:
.
Ортогональность матрицы. Сумма поэлеметных произведений любых двух векторов-столбцов матрицы равна нулю
, где 
.
Ортогональные планы делают эксперимент более эффективным и позволяют получать оценки для коэффициентов уравнения регрессии независимые друг от друга. Иными словами ортогональность характеризует отсутствие связей между факторами.
Коэффициенты 
оцениваются с помощью выражений
, 
, 
.
Однако, если имеет место нелинейность, то столбцы взаимодействий окажутся неразличимы, связанными с некоторыми столбцами линейных эффектов. Это приводит к тому, что по результатам данного эксперимента становится невозможным разделить коэффициенты регрессии между линейными и нелинейными факторами.
Один из часто встречающихся видов нелинейности связан с тем, что эффект одного фактора зависит от уровня, на котором находится другой фактор. В этом случае говорят, что имеет место эффект взаимодействия двух факторов. Полный факторный эксперимент позволяет количественно оценивать эффекты взаимодействия. Для этого надо, пользуясь правилом перемножения столбцов, получить столбец произведения двух факторов. При вычислении коэффициента, соответствующего эффекту взаимодействия, с новым вектор-столбцом можно обращаться так же, как с вектор-столбцом любого фактора. Тогда уравнение принимает вид
(3.4)
Матрица полнофакторного эксперимента с учетом фактора взаимодействия для ПФЭ 22 показана в табл.3.3.
Таблица 3.3
Матрица планирования ПФЭ с учетом парного взаимодействия факторов
| Номер опыта | 
| 
| 
|
|
| -1 | -1 | +1 | y1 | |
| +1 | -1 | -1 | y2 | |
| -1 | +1 | -1 | y3 | |
| +1 | +1 | +1 | y4 |
Коэффициенты уравнений регрессии оцениваются следующим образом:
, , 
, 
.
По столбцам и осуществляют планирование, а столбец 
служит только для расчета.
Для трех факторов матрица ПФЭ 
=8 (табл. 3.4).
Таблица 3.4
Матрица ПФЭ для трех факторов
| Номер |
| 
| 
|
| 
| 
| 
|
|
| опыта | ||||||||
| -1 | -1 | -1 | +1 | +1 | +1 | -1 | y1 | |
| +1 | -1 | -1 | -1 | -1 | +1 | +1 | y2 | |
| -1 | +1 | -1 | -1 | +1 | -1 | +1 | y3 | |
| +1 | +1 | -1 | +1 | -1 | -1 | -1 | y4 | |
| -1 | -1 | +1 | +1 | -1 | -1 | +1 | y5 | |
| +1 | -1 | +1 | -1 | +1 | -1 | -1 | y6 | |
| -1 | +1 | +1 | -1 | -1 | +1 | -1 | y7 | |
| +1 | +1 | +1 | +1 | +1 | +1 | +1 | y8 |
В зависимости от соотношения числа неизвестных коэффициентов уравнения регрессии 
и числа строк в матрице ПФЭ 
план может являться насыщенным, при выборе числа членов уравнения 
, ненасыщенным, при выборе числа членов уравнения и соответственно числа столбцов плана 
и сверхнасыщенным 
.
Во многих реальных процессах некоторые факторы взаимодействия могут отсутствовать. И тогда ПФЭ будет обладать избыточностью опытов. Рассмотрим пути минимизации числа опытов.
Обратимся к уравнению (3.4). Если есть информация о том, что в выбранных интервалах варьирования процесс может быть описан линейной моделью, то достаточно определить три коэффициента . В результате остается одна степень свободы, т.к. имеем четыре опыта, а количество констант три. Используем эту степень свободы для минимизации числа опытов. При линейном приближении 
и тогда вектор-столбец может быть использован для нового фактора .
Таблица 3.5
Матрица планирования дробно-факторного эксперимента
| Номер опыта |
|
|
|
|
| +1 | +1 | +1 | y1 | |
| -1 | +1 | -1 | y2 | |
| +1 | -1 | -1 | y3 | |
| -1 | -1 | +1 | y4 |
При этом эксперименте появляются смешанные оценки
, 
, 
,
которые невозможно отделить от эффектов факторов
Пример. Допустим и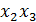 
связаны между собой. Однако парные взаимодействия в линейной модели незначительны. Зато вместо восьми опытов для изучения влияния трех факторов можно поставить только четыре опыта, т.е. вместо ПФЭ 23 имеем 23-1. В теории эксперимента 23-1 называют полурепликой. В общем случае имеют дело с дробной репликой. А факторный эксперимент называют дробным (ДФЭ).
Для составления МПЭ ДФЭ вводится понятие определяющего контраста, которыйпозволяет определить, какие оценки смешаны друг с другом, не изучая МПЭ, для выявления совпадающих столбцов. Для этого используется символичное обозначение произведения столбцов равного +1 или -1. Это и называют контрастом. Чтобы определить какой эффект смешан с данным, нужно помножить обе части определяющего контраста на столбец, соответствующий данному эффекту.
Пример. Пусть имеем три фактора , 
, 
. При построении полуреплики 
имеется только две возможности приравнять либо к « 
», либо к « 
» (табл.3.6).
Таблица 3.6
Матрица планирования дробно-факторного эксперимента
| Опыт |
|
|
|
| Опыт |
|
|
|
|
| -1 | -1 | +1 | +1 | -1 | -1 | -1 | -1 | ||
| +1 | -1 | -1 | +1 | +1 | -1 | +1 | -1 | ||
| -1 | +1 | -1 | +1 | -1 | +1 | +1 | -1 | ||
| +1 | +1 | +1 | +1 | +1 | +1 | -1 | -1 |
Возьмем в качестве определяющего контраста -1= .Тогда - = 
. Учитывая, что 
получаем = 
.
Теперь возьмем за определяющий контраст 1= . Получаем: 
= , 
= , 
= . Эти выражения показывают, что коэффициенты линейного уравнения будут оценками и парных произведений факторов.
Соотношение, показывающее, с какими из эффектов смешан данный эффект, называется генерирующим соотношением.
При выборе полуреплики 24-1 возможны восемь генерирующих соотношений:
| 
|
| 
|
| 
|
| 
|
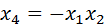
Разрешающая способность этих полуреплик различна. Первые шесть реплик имеют по три фактора и носят название планов с расширяющей способностью 3 (по наибольшему числу факторов в определяющем контрасте). Две последние реплики имеют по четыре фактора и обладают максимальной разрешающей способностью. Их называют главными репликами. Всегда стремятся выбрать реплику с наибольшей разрешающей способностью, т.к. чем больше эффектов взаимосвязано, тем точнее окажется полученная модель.
Однако, если имеется информация об эффектах взаимодействия, то реплики нужно выбирать с ее учетом.
Реализация МПЭ ДФЭ ничем не отличается от реализации МПЭ ПФЭ. Методика оценки значимости коэффициентов и проверка адекватности модели проводится также как и в ПФЭ.
Если при выбранной реплике некоторые коэффициенты получаются отличными от нуля, например: 
, 
то ставят вторую серию опытов с другой репликой.
Дробные реплики находят широкое применение при получении линейных моделей, причем, целесообразность применения их возрастает с ростом количества факторов. Эффективность применения дробных реплик зависит от выбора системы смешивания линейных эффектов с эффектами взаимодействия.
Планирование экспериментов при построении квадратичных регрессионных моделей
Линейные модели или неполные квадратичные не всегда адекватны экспериментальным данным, кроме того их использование не позволяют определить оптимальные значения факторов, поэтому для уточнения экстремальных значений необходимо строить более эффективные модели, которыми и являются квадратичные.
Для двухфакторного эксперимента модель может быть представлена выражением
(3.5)
Векторы - столбцы 
и 
являются единичными столбцами, совпадающие друг с другом. Эти столбцы неразличимы, поэтому нельзя сказать, за счет чего получилась величина 
. Очевидно, она включает в себя как значение свободного члена 
так и вклады квадратичных членов. Символически это можно записать: 
Следовательно, планирование эксперимента на двух уровнях не дает возможности получить раздельные оценки коэффициентов при квадратичных членах и свободного члена 
.
Согласно теории интерполяции, для решения задачи нахождения раздельных оценок число уровней каждой из независимых переменных должно быть на единицу больше степени интерполяционного полинома. Для полинома второй степени число уровней должно быть равно трем.
Однако применение методов ПФЭ плана 
не является рациональным из-за резкого увеличения опытов эксперимента. Поэтому были разработаны специальные методы построения планов второго порядка, которые нашли широкое применение в инженерной практике. Такие планы называются центральными композиционными (ЦКП): понятие «центральные» означает симметричность точек плана относительно его центра; понятие «композиционный» отражает свойство компановки нового плана путем добавления опытов к плану ПФЭ или ДФЭ. Основным преимуществом таких планов является возможность использования результатов опытов, полученных ранее при построении линейных моделей.
Ядром ЦКП является план ПФЭ 
или ДФЭ 
. К этому ядру добавляются «звездные точки» в количестве 
и «нулевая точка», количество опытов в которой увеличивается для повышения точности эксперимента.
Общее количество опытов при ЦКП определяется по формуле:
(3.6)
где 
- число опытов ПФЭ ил ДФЭ; 
- число опытов в центре плана; 
- число звездных точек.
Например, в качестве двухфакторных планов второго порядка могут служить планы, представляемые вершинами и, по крайней мере, одной центральной точкой любого 
мерного правильного многоугольника (который можно вписать в круг). «Звёздные» точки с координатами 
и 
лежащие на сфере диаметра 
. Величину 
называют звездным плечом, которое равно расстоянию от центра плана до «звездной» точки. Графическое изображение такого плана эксперимента приведено на рис.3.4., а в таблице 3.7 приведена упрощенная матрица планирования для ЦКП 2-ого порядка при . 
и величиной звездного плеча 
.
|
|
|
|
| (0,0) |
| -1 |
| -1 |
| L |
| A |
| M |
| D |
| C |
| K |
| B |
| N |
Рисунок 3.4 - Восьмиугольный план эксперимента
Таблица 3.7
| Номер опыта |
|
| Описание |
| -1 | -1 | План 22 | |
| +1 | -1 | представлен | |
| -1 | +1 | квадратом | |
| +1 | +1 | АВСD | |
| Ö2 | План | ||
| -Ö2 | представлен | ||
| Ö2 | звёздными точками | ||
| -Ö2 | MNKL | ||
| Центральная точка |
Добавление звездных и центральной точек к ПФЭ позволяет получить раздельные оценки и 
.
В зависимости от критерия оптимальности плана, различают ортогональное и рототабельное композиционное планирование.
Ортогональные планы оптимальны с точки зрения простоты обработки полученной информации: все оценки коэффициентов уравнения регрессии определяют независимо друг от друга, незначимые коэффициенты отбрасываются без перерасчета оставшихся значимых. Величина «звездного» плеча в таких планах равна единице.
Анализ результатов экспериментов при ортогональном композиционном планировании имеет некоторые особенности. Так оценки коэффициентов уравнения регрессии находятся с неодинаковой дисперсией.
Из-за неодинаковой дисперсии коэффициентов регрессии критерий ортогональности является недостаточно сильным критерием оптимальности для планирования второго порядка. Поэтому точность предсказания выходной величины в различных направлениях факторного пространства неодинакова. Лучшим методом планирования является такой метод, который обеспечивает одинаковую точность во всех направлениях на одинаковом расстоянии от центра. Таким методом является рототабельное композиционное планирование
Рототабельные планы(РЦКП) обеспечивают одинаковую точность и постоянную дисперсию экспериментальных данных во всех напрвлениях на равных расстояних от центра плана: 
при одинаковом удалении точек эксперимента от центра, т.е. точки находятся на поверхности сферы радиусом 
План, приведенный в табл. 3.7, является рототабельным и обеспечивает получение раздельных оценок и .
Величина «звездного» плеча определяется из соотношений:
при 
при 
.
Для обеспечения точности эксперимента число центальных точек выбирают в зависимости от ядра плана. Параметры РЦКП приведены в таблице 3.8.
Таблица 3.8
| n | Ядро плана | Число «звездных» точек | N0 | N | a |
| 2 |
| 4 | 5 | 13 | 1,414 |
| 3 | 
| 6 | 6 | 20 | 1,682 |
| 4 | 
| 8 | 7 | 31 | 2,000 |
| 5 | 
| 10 10 | 10 6 | 52 32 | 2,378 2,000 |
| 6 | 
| 12 12 | 15 9 | 91 53 | 2,828 2,378 |
| 7 | 
| 14 14 | 21 14 | 163 92 | 3,333 2,828 |
Матрица планирования рототабельного плана второго порядка для трехфакторного эксперимента представлена в таблице 3.9.
Таблица 3.9
Матрица рототабельного планирования 3-факторного эксперимента
| Номер |
|
|
| 
| 
| 
| 
| 
|
|
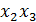
| опыта | |||||||||
| -1 | -1 | -1 | +1 | +1 | +1 | +1 | +1 | +1 | |
| +1 | -1 | -1 | +1 | +1 | +1 | -1 | -1 | +1 | |
| -1 | +1 | -1 | +1 | +1 | +1 | -1 | +1 | -1 | |
| +1 | +1 | -1 | +1 | +1 | +1 | +1 | -1 | -1 | |
| -1 | -1 | +1 | +1 | +1 | +1 | +1 | -1 | -1 | |
| +1 | -1 | +1 | +1 | +1 | +1 | -1 | +1 | -1 | |
| -1 | +1 | +1 | +1 | +1 | +1 | -1 | -1 | +1 | |
| +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | |
| -1,682 | 2,828 | ||||||||
| +1,682 | 2,828 | ||||||||
| -1,682 | 2,828 | ||||||||
| +1,682 | 2,828 | ||||||||
| -1,682 | 2,828 | ||||||||
| +1,682 | 2,828 | ||||||||
Эксперимент проводится аналогично ПФЭ, однако оценки коэффициентов рассчитываются по следующим формулам:
где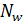 
- число точек на сфере радиуса 
; 
- число сфер 
.
Проверка значимости коэффициентов уравнения и адекватности модели будет рассмотрен ниже.
Дата добавления: 2014-11-13; просмотров: 621; Мы поможем в написании вашей работы!; Нарушение авторских прав |