Определение области оптимума функции отклика второго порядка

Функция отклика, соответствующая многофакторной регрессионой модели второго порядка, а общем случае предсталяет собой следующее соотношение:

(3.7)

Поверхность, которая является геометрическим образом функции отклика в 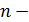мерном пространстве, называется гиперповерхностью.

Для нахождения координат точки гиперповерхности, являющейся ее экстремумом, необходимо приравнять нулю частные производные от функции отклика по всем факторам и решить систему из линейных алгебраических уравнений относительно факторов:

. (3.8)

Подставляя найденные координаты 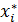в функцию отклика, вычисляют ее значение в точке экстремума. Это значение может находиться как в области изменения всех факторов, так и в области изменения части факторов, а также может находиться вне области изменения факторов и даже вне области их определения. Во все случаях, за исключением первого, об области экстремума невозможно сделать определенных выводов без дальнейшего исследования гиперповерхности отклика.

Планирование эксперимента при поиске оптимальных условий

Во многих случаях инженерной практики перед исследователем ставится задача не только выявления связи между рядами наблюдений, но и нахождение таких численных значений факторов при которых отклик (выходной параметр) достигает своего экстремального значения. Эксперимент, решающий эту задачу, называется экстремальным. В этом случае задача сводится к оптимизационной и формулируется следующим образом: требуется определить такие координаты экстремальной точки ( поверхности отклика , в которой она максимальна (минимальна).

Разработано множество методов пошаговой оптимизации, мы же рассмотрим некоторые, которые эффективно используются в промышленном и лабораторном эксперименте.