КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Кодирование факторов при подготовке эксперимента
Если заранее не известно аналитическое выражение функции отклика 
, то можно рассматривать не саму функцию, а ее разложение, например, в степенной ряд в виде полинома (3.1).
Разложение в степенной ряд функции возможно в том случае, если сама функция является непрерывной. На практике обычно ограничиваются числом членов степенного ряда и аппроксимируют функцию полиномом некоторой степени.
| Рисунок 3.3 - Координаты исходных и кодированных факторов |
|
| X1max |
| X1min |
| X1ср |
|
|
|
| X2 |
| X1min |
| X1max |
| X1ср |
| X1 |
| +1 |
| +1 |
| -1 |
| -1 |
используют кодирование факторов.
Эта операция заключается в выборе нового масштаба для кодированных факторов (рис. 3.3), причем такого, чтобы минимальное значение кодированных факторов соответствовало “-1”, а максимальное значение “+1”, а также в переносе начала координат в точку с координатами 
.
Текущее значение кодированного фактора
, (3.2)
где 
– именованное (абсолютное) значение фактора; 
– кодированное значение фактора; 
- интервал варьирования 
фактора.
Если фактор изменяется дискретно, например он является качественным, то каждому уровню этого кодированного фактора присваиваются числа в диапазоне от +1 до –1. Так при двух уровнях это +1 и –1, при трех уровнях +1, 0, -1 и т.д.
Функция отклика может быть выражена через кодированные факторы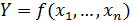 
и записана в полиномиальном виде
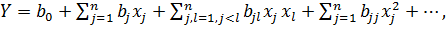(3.3)
Очевидно, что 
, но
Для полинома, записанного в кодированных факторах, степень влияния факторов или их сочетаний на функцию отклика определяется величиной их коэффициента 
. Для полинома в именованных факторах величина коэффициента 
еще не говорит однозначно о степени влияния этого фактора или сочетаний факторов на функцию отклика.
Задача определения коэффициентов уравнения регрессии. Для определения 
коэффициента полинома необходимо не менее уравнений (опытов).
Полученные коэффициенты 
позволяют сформировать функцию отклика при слагаемых правой части. Если точность этой функции оказалась недостаточной, то требуется взять многочлен с большим числом членов и начать все заново, так как все коэффициенты оказываются зависимыми друг от друга. Это возникает при использовании пассивного эксперимента. Однако если целенаправленно использовать активный эксперимент, и особым образом построить матрицу сочетаний факторов в опытах 
, используя планирование эксперимента, то коэффициенты полинома будут определены независимо друг от друга.
Стратегия применения планов заключается в принципе постепенного планирования – постепенного усложнения модели. Начинают с простейшей модели, находятся для нее коэффициенты, определяется ее точность. Если точность не удовлетворяет, то планирование и модель постепенно усложняются.
Дата добавления: 2014-11-13; просмотров: 327; Мы поможем в написании вашей работы!; Нарушение авторских прав |