Собственные затухающие колебания

Если вследствие внутреннего трения, сопротивления воздуха и т.п. энергия колебательной системы постоянно уменьшается, то и амплитуда колебания в конечном счете уменьшится до нуля. Поэтому амплитуда в данном случае есть функция времени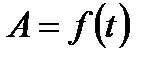

Затухание вызывается силой, которая пропорциональна скорости (для не очень больших скоростей) и направлена противоположно ей (см. 3.16):

, где r - коэффициент сопротивления.

Используя уравнение движения , в котором , имеем: или .

Деля это равенство на массу и вводя понятие коэффициента затухания , получим дифференциальное уравнение затухающих колебаний:

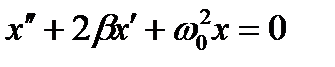. (6.23)

Общим решением этого уравнения является:

, (6.24)

где

(6.26)

T= (6.26’)

здесь A_з и - амплитуда и циклическая частота затухающих колебаний.

Натуральный логарифм отношения амплитуд предыдущего колебания к соседнему последующему называется логарифмическим декрементом затухания (см.рис.6.4), т.е.

Величина, обратная показывает число колебаний, совершаемых за время, в течение которого амплитуда уменьшится в e = 2,72 раза:

. (6.28)

где I - момент инерции физического маятника относительно оси вращения.

Для малых отклонений имеем

Обозначив , (6.19) придем к выражению, подобному (6.8):

, (6.20)

которое является дифференциальным уравнением колебаний физического маятника. Решением его будет: .

С физической точки зрения формулы (6.10), (6.13) и (6.20) идентичны. Это объясняется тем, что все они отражают свободные незатухающие колебательные движения (внешние силы отсутствуют).

Из уравнения (6.19) с учетом (6.4) получим выражение для периода колебания физического маятника

, (6.21) где - приведенная длина физического маятника.

Сопоставляя (6.21) с формулой (6.15) находим, что математический маятник с длиной l будет иметь такой же период колебаний, как и данный физический маятник, с длиной l_пр.