На составляющие.

Каждый вектор можно заменить несколькими векторами 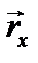, , 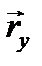, 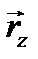…., которые в сумме дают вектор 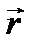.В этом случае 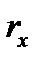, , 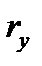, 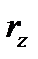и т.д. называются составляющими вектора .

Проекции вектора на оси декартовой системы координат показаны на рис.1.4.

z

x = | |·cos α,

z y = | |·cos β,

γ z = | |·cos γ . (1.4)

0 α x

y β x

y

Рис. 1.4.

Радиусом-вектором точки называется вектор (см. рис. 1.4), проведённый из начала координат в данную точку. Радиус-вектор однозначно определяет положение точки в пространстве.

где знак минус учитывает противоположные направления перемещения (смещения) и силы F_y, a 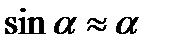, т. к. первоначально маятник был отклонен на малый угол.

С другой стороны, F_y- можно определить по второму закону Ньютона: 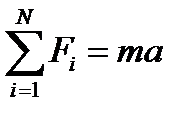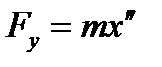, или .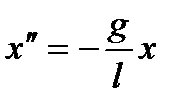

Тогда 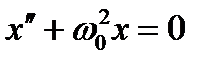, (6.13)

где 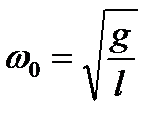. (6.14)

Выражение (6.13) является дифференциальным уравнением колебаний математического маятника, решением которого будет

.

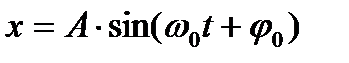Учитывая (6.4) и подставляя вместо 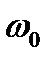её значение из (6.14) получим формулу для периода колебаний математического маятника:

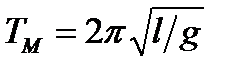. (6.15)

Заметим, что период математического маятника не зависит не только от амплитуды (изохронность), но и от массы маятника.

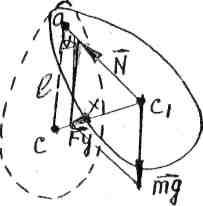
6.3.3. Физический маятник - это любое тело (не представляющее собой материальную точку), колеблющееся относительно оси, которая не проходит через центр инерции С (рис.6.3).

Если центр инерции расположен на расстоянии l от оси вращения, то момент силы тяжести

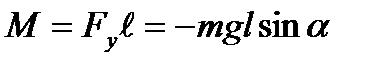. (6.16)

Этот момент силы заставляет отклоненный маятник вернуться в исходное состояние и продолжить движение в другую сторону, поэтому уравнение его движения будет иметь вид:

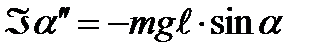. (6.17)

Здесь учтен основной закон вращательного

движения:

Рис.6.3. , (6.18)