Табличные формулы.

Выше мы уже упоминали, что понятие производной и интеграла в физике несколько отличается от математического. Однако это не влияет на процесс решения и результаты дифференцирования и интегрирования, т. е. все формулы высшей математики справедливы (табл. 1.4)

Таблица 1.4

Дифференцирование Интегрирование .

(ax)' = a(x' = 1) ∫dx = x+C

(aU)' = aU' x₂

(xⁿ)' = n·x ^n-1 ∫dx = x₂ – x₁ = x

(ℓn x)' = 1/x x₁

(ℓn U)' = U' /U

(U·V)'= U·V'+V·U' ∫ xdx = (x²/2)+C

U '_ U'·V – U·V'

V ¯ V² ∫xⁿdx = ((xⁿ+1)/(n+1))+C (n ≠ - 1)

(e^ах)' = ае^ах х₂

(sin x)'= cos x ∫xdx = x²₂/2 – x²₁/2

(sin ω t)'= ω·cos ωt x₁

(cos x)'= – sin x ∫е^ахdx = (e^ax/а)+С

∫ dx/x = ℓn x+C

∫ sin ωt·dt = –( cos ωt / ω)+C

∫ cos ax·dx = (sin ax / a)+C

С производными и неопределенными интегралами студенты уже встречались, поэтому несколько подробнее расскажем об определенном интеграле. Если результат неопределённого интегрирования справедлив с точностью до некоторой постоянной С, то в результате «взятия» определённого интеграла получается точный ответ, поскольку интегрирование в этом случае ведётся в заданных (конечных) пределах. Эти пределы указываются под интегралом (начальная величина) и над интегралом (конечная). После решения интеграла (правила те же,

где k - коэффициент упругости (жесткости) пружины.

Механическая система, совершающая колебания около положения равновесия, называется классическим осциллятором. Примерами гармонического осциллятора являются колебания груза, подвешенного на пружине, математического и физического маятников.

Минимальный промежуток времени; по истечении которого движение повторится, называют периодом колебаний Т. Число полных колебаний за одну секунду носит название частотыV:

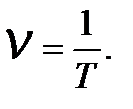
(6.3)

В теории колебаний используют также циклическую частоту ω:

. (6.4)