Свободные незатухающие колебания.

Как и все механические движения, гармонические колебания подчиняются второму закону Ньютона (см. (3.2)). Если масса осциллятора неизменна (что в большинстве случаев и имеет место),

то удобнее пользоваться выражением для любого вида колебательного движения.

Рассмотрим закономерности свободных незатухающих колебаний нa примере идеальных маятников (пружинного, математического и физического), на которые не действуют никакие силы сопротивления.

6.3.1. Пружинный маятник представляет собой груз массой m, подвешенный на абсолютно упругой пружине и совершающий колебания под действием силы упругости Fy = - kx (см.(6.2)).

Уравнение колебательного движения при этом

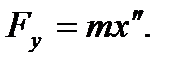, (6.9)

Учтя (6.2), получим 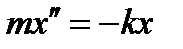или .

Если обозначить , (6.9’)

тогда будем иметь , (6.10)

то есть колебания данного осциллятора - незатухающие. Из (6.9’)

имеем (6.11)

Использовав (6.4), найдем период колебания пружинного маятника

(6.12)

α - мал

6.3.2. Математический маятник - это

идеализированная система, состоящая из

материальной точки, подвешенной на

длинной нерастяжимой нити (рис.6.2).

На отклоненный из положения

равновесия математический маятник

действует сила:

,

1.6.5. Скалярное произведение двух векторов r₁ и r₂ определяется как скаляр (число).

r = ( · ) = | | · | |·cos = r₁·r₂·cos, (1.5)

где  – угол между векторами.

Свойства скалярного произведения

( · ) = ( · ); ·(a · + b · r₃) = a·( · ) + b·( · r₃), (1.6)

( )² = ( · ) = | | · | |·cos  = | | · | |·cos 0 = r².

Таким образом, квадрат вектора есть скаляр.

Если два вектора перпендикулярны друг другу (ортогональны),

то ( · ) = 0,  = π / 2, 3π / 2, …, (1.7)

если параллельны, то ( · ) = + r₁· r_2,  = 0, (1.8)

если антипараллельны, то ( · ) = – r₁· r_2,  = π. (1.9)

Не существует действия, обратного скалярному умножению векторов, т.е. деление на вектор – это не имеющая смысла неопределенная операция.