
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Кинематика колебательного движения
Напомним, что кинематика изучает движения тел в отсутствии внешних сил, такие, например, как незатухающие колебания.
Если собственные незатухающие гармонические колебания описываются уравнением
 , (6.5)
, (6.5)
где A - амплитуда, y0 - начальная фаза, ω0 - циклическая частота незатухающих колебаний, то скорость
 , (6.6)
, (6.6)
а ускорение
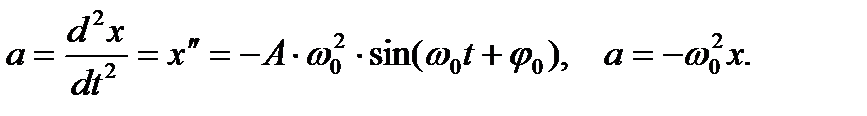 (6.7)
(6.7)
Сравнивая (6.5) и (6.7), получаем дифференциальное уравнение незатухающих колебаний:

 (6.8)
(6.8)
Примечание. В некоторых учебниках первую и вторую производные обозначают:  и
и 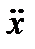 .
.
6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
Основные понятия
Колебательные движения - это движения, обладающие той или иной степенью повторяемости во времени (движения, совершаемые системой относительно некоторого среднего значения).
Колебания свойственны практически всем явлениям природы. В технике они либо выполняют определенные функциональные обязанности (различные маятники), либо возникают как неизбежное проявление физических свойств (вибрации машин и сооружений). В физике особо выделяются механические, электромагнитные колебания и их комбинации.
По характеру воздействия на систему колебания разделяют на свободные (собственные) и вынужденные. Свободные колебания происходят в системе, предоставленной самой себе после того, как она предварительно была выведена из положения равновесия. Вынужденные колебания возникают, когда система постоянно подвергается воздействию периодически повторяющейся внешней силы.
В свою очередь свободные колебания бывают незатухающими и затухающими.
Незатухающие колебания - это колебания, совершающиеся в отсутствии внешних сил.
Затухающими называют колебания, энергия которых уменьшается с течением времени.
Колебания, совершающиеся по закону синуса или косинуса (см. рис.6.1.), называются гармоническими:
 , (6.1)
, (6.1)
| Т |
| А |
| А |
| х |
| t |
| х |
отклонение (А = xmax)
колеблющегося тела от положения
равновесия; 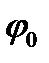 – начальная фаза
– начальная фаза
колебания (при t = 0),

[  ] = рад.
] = рад.
. Отличительным признаком
. гармонических колебаний
Рис. 6.1. является пропорциональность
возвращающей силы или силы упругости Fy смещению системы x:
Fy = - kx, (6.2)
что и для неопределённого) следует подставить пределы интегрирования – сначала верхний, затем нижний и из первого результата вычесть второй:
x2 x2
∫dx / x = ℓn x| = ℓn x2 – ℓn x1 = ℓn (x2 /x1). (1.12)
х1 х1
Дата добавления: 2014-10-31; просмотров: 1157; Мы поможем в написании вашей работы!; Нарушение авторских прав |