Полный дифференциал.

Допустим, имеется физическая величина U(x, y, z, t), зависящая не только от координат x, y, z, но и от времени t, тогда полным дифференциалом называют величину

dU = (∂U / ∂x)dx + (∂U / ∂y)dy + (∂U / ∂z)dz + (∂U / ∂t)dt. (1.13)

Для стационарной, не зависящей от времени функции

dU = (∂U / ∂x)dx + (∂U / ∂y)dy + (∂U / ∂z)dz. (1.14)

Дифференцирование векторных физических величин.

Векторы подчиняются тем же правилам дифференциального исчисления, что и скаляры, но с учётом правил векторной алгебры. Производная от векторной величины r (t) по скалярной переменной t есть вектор

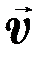= d /dt = ℓim (∆ /∆t) = . (1.15)

∆t→0

Производная от произведения скаляра а(t) на вектор (t) есть вектор

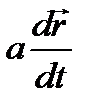. (1.16)

Производная от скалярного произведения двух векторов r₁(t) и r₂(t) есть скаляр

(1.17)

Производная от векторного произведения векторов r₁(t) и r₂(t) есть вектор

. (1.18)

Интегральные и дифференциальные физические