Векторное произведение двух

Векторных величин.

Если из двух векторов и в трехмерном пространстве образовать векторное произведение [ · ], то оно будет вектором , модуль которого равен площади образованного векторами и параллелограмма (рис. 1.5.):

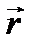= [ · ]; | | = | | · | | · sin α, (1.10)

где α – угол между векторами и .

Вектор перпендикулярен к и :

[ ·[ · ]]=[r₂·[ · ]] = 0, (1.11)

а направление определяется по правилу буравчика (правого винта).

Числ.

S = |[ · ]| = | |.



S

Рис. 1.5.

Чтобы найти направление результирующего вектора необходимо: 1) расположить буравчик перпендикулярно вектору и вектору 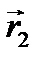(см. рис. 1.5.); 2) вращать ручку буравчика по кратчайшему пути от вектора, стоящего на первом месте в векторном произведении ( ) к другому вектору ( ); 3) поступательное движение буравчика укажет направление вектора .

Дифференцирование и интегрирование физических величин.