Величины.

Интегральными называют физические величины, характеризующие свойства веществ или полей, усреднённые по геометрическим параметрам (объёму, площади, длине). Например, сопротивление R = ρ·ℓ/S (где ℓ и S – длина и площадь поперечного сечения проводника, ρ – удельное сопротивление), сила тока = j·S или точнее (где j – плотность тока).

Дифференциальные физические величины характеризуют свойства вещества или поля в какой-то их точке (в очень малых объёме, площади или длине). Например, напряжённость и потенциал гравитационного или электрического полей, плотность электрического тока ( ), удельное сопротивление проводника и т. д.

относительных скоростей шаров после соударения и до соударения называют коэффициентом восстановления: .

Если ε = 0, то удар абсолютно неупругий, если ε = 1, то абсолютно упругий.

При абсолютно неупругом ударе часть механической энергии переходит в другие формы энергии (например, в тепловую). В этом случае выполняется лишь закон сохранения импульса, на основании которого и находим скорость шаров после столкновения;

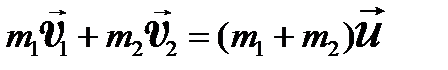; . (5.25)

Найдем изменение кинетической энергии шаров, т.е. ту ее часть которая перешла во внутреннюю энергию, что приводит к нагреванию(диссипации – рассеянию).

. (5.26)

При абсолютно упругом ударе потерь энергии нет, и в этом случае выполняются законы сохранения импульса и энергии:

. (5.27)

Решая систему этих уравнений, находим:

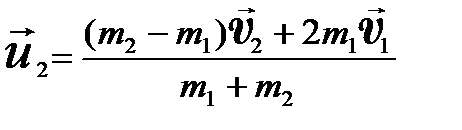; . (5.28)

Когда массы соударяющихся тел равны: m₁ = m₂, то шары обменивается скоростями: , .

5.8. Энергия вращательного и плоского движений.

Кинетическая энергия вращательного движения

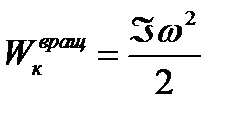(сравните ).

Кинетическая энергия плоского движения

( – скорость центра масс).

При этом .

Перемножим почленно каждое из равенств (5.22) и (5.23):

, .

Сложив их, получим:

.

Так как , a (см.(5.12)),

то ,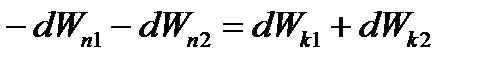

или .

Обобщим этот результат на случай нескольких взаимодействующих тел. Обозначив через и - суммарные кинетическую и потенциальную энергии, будем иметь: . Воспользовавшись правилом дифференцирования: , придем к окончательному результату:

, (5.24)

где механическая энергия всех тел системы

Формула (5.24) является математическим выражением закона сохранения механической системы: механическая энергия консервативной системы остаётся постоянной.

Этот закон связан с однородностью времени, то есть с инвариантностью физических законов относительно выбора начала отсчета времени. Так, при свободном падении тела в гравитационном поле его скорость и перемещение зависят от начальной скорости и продолжительности падения, но не зависят от того, когда тело начало падать.