Потенциальная энергия гравитационного притяжения двух тел

Рассмотрим два тела (являющиеся материальными точками) массами m₁ и m₂, притягивающиеся друг к другу (например, камень и Земля) с силой .

При приближении этих тел будет производиться положительная работа. В соответствии с (5.11) имеем:

. (5.17)

положения 1 в положение 2 (рис. 2.2). Очевидно, что перемещение

∆ = – . (2.2)

1 Разделив ∆ на соответствующий

промежуток времени ∆t , получим

3 вектор средней скорости:

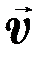
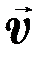_ср = ∆ / ∆t. (2.3)

∆ Кроме этой скорости, средней для

2 участка пути 1 – 2, используют в той

или иной точке пути (например, в

0 положении 3), называемую мгновенной

Рис. 2.2. скоростью. Из высшей математики известно, что для определения мгновенной скорости нужно взять предел средней скорости при ∆t→0:

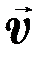=ℓim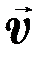_ср = ℓim ∆ /∆t = d /dt. (2.4)

∆ t→0 ∆ t→0

Таким образом, вектор мгновенной скорости равен производной по времени от радиуса-вектора движущейся материальной точки. Так как в пределе длина хорды |d | стремится к длине стягиваемой дуги dℓ, то модуль скорости

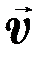=||= |d | /dt = dℓ /dt = ds/ t (2.5)

Направление вектора скорости 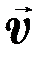есть, как требует определение (2.4), предел направления хорды (совпадающей по направлению с ∆ ) при уменьшении ее длины (стягивании в точку). А это есть направление касательной к траектории.

Следовательно, в общем случае вектор мгновенной скорости в каждой точке траектории касателен к ней.

Физический смысл скорости: скорость – векторная физическая величина, характеризующая быстроту изменения перемещения материальной точки в пространстве.

При произвольном движении вектор скорости 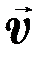непрерывно меняется как по величине, так и по направлению (рис. 2.3).

Векторная физическая величина, характеризующая быстроту изменения скорости, называется ускорением .

Формулу для определения ускорения неравномерного криволинейного движения можно получить из следующих соображений. Если обозначить скорость материальной точки в вектор 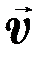₂ в точку А параллельно самому себе, можно найти приращение ∆:

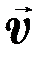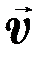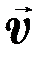∆= ₂ –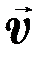₁ . (2.6)

Разложим вектор ∆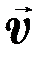на два составляющие:

вектор ∆ 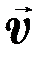_t – касательный

А 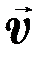₁ к траектории рассматриваемой

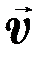С кривой и вектор _n –

перпендикулярный ∆ , то есть

В направленный к центру кривизны

траектории О. При этом

∆ ∆ = +∆ . (2.7)

D Среднее ускорение за

промежуток времени ∆t:

О Рис. 2.3.

= ∆/∆t = /∆t + ∆/∆t. (2.8)

Мгновенное ускорение:

=ℓim =ℓim/∆t + ℓim ∆/∆t = + , (2.9), где введены обозначения: =ℓim/∆t, =ℓim ∆/∆t. (2.10)

∆ t→ 0 ∆ t→ 0

Вектор носит название нормального (или центростремительного) ускорения, вектор называют тангенциальным (или касательным) ускорением. Эти названия следуют из выражений (2.10), поскольку ∆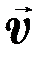_n нормален, а ∆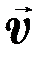_t касателен к траектории.

Модуль нормального ускорения можно определить по рис.2.3, учтя, что треугольник AOD и АВС подобны:

а_n =| 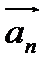| = / r, (2.11)

где r – радиус кривизны траектории. (Вывод этой формулы представляется сделать студентам самостоятельно).

Надо отметить, что уравнение (2.11) является общим, то есть справедливым для движения по любой кривой: эллипсу, параболе, окружности и др., а также для равномерного, равнопеременного и неравномерного движений. Это вытекает из того, что при выводе (2.11) не было наложено никаких ограничений на вид траектории и характер движения.

Модуль тангенциального ускорения а_t =| 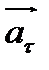| = d /dt. (2.12)

Нормальное и тангенциальное ускорения зависят от вектора скорости неоднозначно. Так, нормальное ускорение возникает только при изменении направления скорости, а тангенциальное ускорение – при изменении модуля скорости.

По второму закону Ньютона 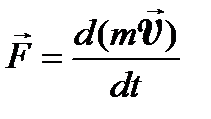. Решая систему уравнений (5.11), получаем:

Опуская индексы, имеем (при m=const) (5.13).

Этот же результат получим при предположении, что тело начало движение из состояния покоя.

Если А > 0, то W_k2 > W_k1 , то есть положительная работа внешней силы увеличивает кинетическую энергию тела. Наоборот, при А < 0 W_k2 < W_k1, то есть отрицательная работа внешних сил выступающих как силы сопротивления или торможения, уменьшает кинетическую энергию.