
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Кинематика абсолютно твердого тела
Абсолютно твердое тело (в дальнейшем – твердое тело) можно представить как совокупность большого числа материальных точек, жестко связанных между собой.
Простейшими видами механического движения твердого тела являются поступательное и вращательное.
При поступательном движении все точки твердого тела движутся одинаково. Для описания такого движения справедливы все уравнения, которые были получены для поступательного движения
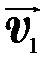 материальной точки. При этом в твердом теле можно выбрать любую
материальной точки. При этом в твердом теле можно выбрать любую
точку, которую обычно называют полюсом.
Прежде чем перейти к рассмотрению
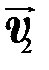

 вращательного движения твердого тела,
вращательного движения твердого тела,
 целесообразно ввести понятие: число степеней
целесообразно ввести понятие: число степеней
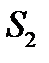 свободы (ЧСС) - число независимых
свободы (ЧСС) - число независимых
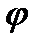
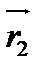 всевозможных перемещений механической
всевозможных перемещений механической
системы. Количество уравнений, с помощью
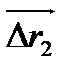
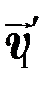
 равно числу степеней свободы. Так, для
равно числу степеней свободы. Так, для
свободной материальной точки ЧСС равно трём,
Рис. 2.6. возможных кинематических уравнений также 3:
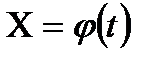 ;
;  ;
; 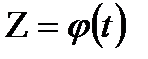 .
.
Вращение вокруг неподвижной оси - это движение, при котором все точки твердого тела описывают концентрические окружности, центры которых лежат на одной прямой, называемой осью вращения (см. рис.2.6). Тело, вращающееся вокруг неподвижной оси, имеет одну степень свободы и описывается одним уравнением: 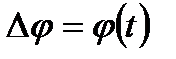 , где
, где 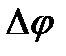 – угловое перемещение.
– угловое перемещение.
Чем дальше отстоят от оси вращения тела его точки, тем большие пути (  >
> 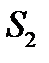 ) они проходят за один и тот же промежуток времени, тем больше перемещение (
) они проходят за один и тот же промежуток времени, тем больше перемещение ( 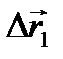 >
> 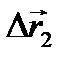 ) и линейная скорость (
) и линейная скорость ( 
 >
> 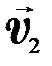 ) Поэтому-то и неудобно пользоваться для описания вращательного движениям этими физическими величинами, а необходимо переходить к угловым
) Поэтому-то и неудобно пользоваться для описания вращательного движениям этими физическими величинами, а необходимо переходить к угловым 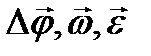 , для определения которых следует пользоваться формулами ((2.19) - (2.25)).
, для определения которых следует пользоваться формулами ((2.19) - (2.25)).
Более сложным случаем вращательного движения является движение твердого тела вокруг неподвижной точки О. В этом случае все точки тела движутся по поверхностям концентрических сфер, центры которых находятся в точке О, а само твердое тело имеет 3 степени свободы: оно может совершать независимые перемещения вокруг трех взаимно перпендикулярных неподвижных осей, проходящих через точку О. Поэтому для однозначного задания положения такого тела в пространстве необходимо иметь три независимые величины. Обычно для этого используют три угла:  .
.
В самом общем случае твердое тело имеет 6 степеней свободы (3 - соответствуют поступательным движениям вдоль трех осей координат и 3 - вращениям вокруг этих осей). Такое движение называется сложным. Оно должно описываться шестью уравнениями.
Частным случаем сложного движения является плоскопараллельное илиплоское движение(например, качение цилиндра по плоской поверхности), при котором все точки тела движутся в параллельных плоскостях. Плоское движение можно представить как совокупность поступательного движения со скоростью  и вращения с угловой скоростью
и вращения с угловой скоростью  :
:  ,
,
где 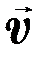 - скорость точек твердого тела относительно неподвижной системы отсчета;
- скорость точек твердого тела относительно неподвижной системы отсчета;  - скорость, обусловленная вращением тела;
- скорость, обусловленная вращением тела; 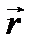 - радиус-вектор, проведенный из центра вращения (или из полюса) в данную точку.
- радиус-вектор, проведенный из центра вращения (или из полюса) в данную точку.
потенциальной энергии взаимодействия тела с Землёй. 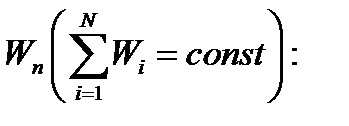
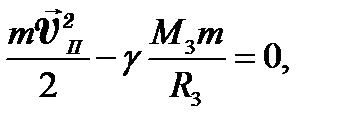
откуда 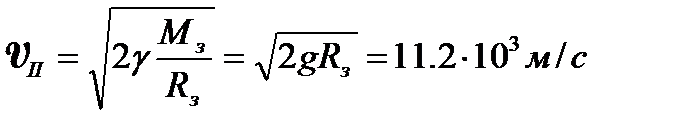 , (4.23)
, (4.23)
где 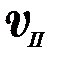 – вторая космическая скорость. Тело, запущенное с такой скоростью с поверхности Земли, становится спутником Солнца. Траектория движения тела в этом случае – парабола.
– вторая космическая скорость. Тело, запущенное с такой скоростью с поверхности Земли, становится спутником Солнца. Траектория движения тела в этом случае – парабола.
Первую космическую скорость  – скорость, необходимую для запуска искусственного спутника Земли, можно определить, пользуясь 2-ым законом Ньютона (предлагается вывести студентам самостоятельно):
– скорость, необходимую для запуска искусственного спутника Земли, можно определить, пользуясь 2-ым законом Ньютона (предлагается вывести студентам самостоятельно): 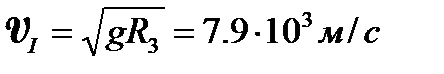 . (4.24)
. (4.24)
Наконец, чтобы преодолеть притяжение не только Земли, но и Солнца, тело должно получить 3-ю космическую скорость: 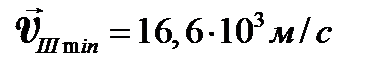
5. РАБОТА СИЛЫ. МОЩНОСТЬ. ЭНЕРГИЯ
Дата добавления: 2014-10-31; просмотров: 386; Мы поможем в написании вашей работы!; Нарушение авторских прав |