Гравитационное поле.

Гравитационное взаимодействие осуществляется посредством центрального гравитационного поля (поля тяготения).

Для количественной характеристики гравитационного поля вводят две физические величины - напряженность и потенциал поля тяготения.

Напряженность гравитационного поля Н - векторная физическая величина, равная по величине и направлению силе, действующей на единичную массу, помещенную в данную точку поля. Но из второго закона Ньютона следует, что если силу разделить на массу тела, на которое она действует, то получим ускорение. Таким образом, напряженность гравитационного поля - не что иное, как ускорение силы тяжести.

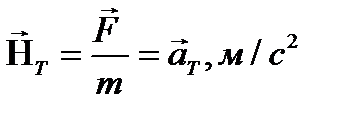. (4.12)

Направлена напряженность Н (как и ускорение) к телу, создающему гравитационное поле. Материальная точка массой m создает гравитационное поле напряженностью

, (4.13)

или в скалярной форме . (4.13')

Модуль напряженности поля Земли в точке, удаленной на расстояние 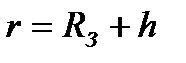от ее центра,

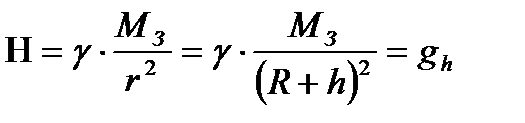, (4.14)

где и – масса и радиус Земли, – расстояние от поверхности Земли до точки.

На поверхности Земли или при имеем

. (4.15)

Уравнение (4.14) позволяет определять напряженность поля и ускорение свободного падения вне Земли. Прежде чем искать зависимость изменения напряженности Н внутри Земли (или любого другого однородного шара), учтем, что гравитационное поле внутри

При неизменной массе тела (m = const): 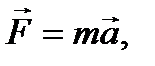(3.3)

где – ускорение тела.

Если на тело действует несколько сил , то в (3.2) и (3.3) подразумевается равнодействующая этих сил:

. (3.4)

Разделив в уравнении (3.2) переменные и проинтегрировав его, получим , (3.5)

где – носит название импульса силы, а – изменение импульса тела( ).

Используя (3.3), можно получить единицу измерения силы:

Третий закон Ньютона: силы, с которыми два тела действуют друг на друга, равны по модулю и противоположны по направлению:

. (3.6)

Но следует иметь ввиду, что эти силы приложены к разным телам.

Использовав (3.5) и (3.6), получим или

, то есть ускорения двух взаимодействующих тел обратно пропорциональны их массам и направлены в противоположные стороны.

Все законы Ньютона справедливы только в инерциальных системах отсчета.