
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Законы классической механики Ньютона
Законы Ньютона - результат обобщения многочисленных опытных данных.
Первый закон Ньютона - это принцип инерции Галилея: всякое тело сохраняет состояние покоя или равномерного прямолинейного движения, пока внешние воздействия не изменят этого состояния.
Второй закон Ньютона утверждает, что скорость изменения импульса пропорциональна приложенной к телу силе. Так как в СИ коэффициент пропорциональности равен единице, то
 (3.2)
(3.2)
полой сферы независимо от толщины ее стенки равно нулю (предлагается студентам доказать это).
Рассмотрим однородный шар радиусом  (см. рис. 4.2.). Мысленно проведем внутри шара сферическую поверхность радиусом
(см. рис. 4.2.). Мысленно проведем внутри шара сферическую поверхность радиусом  .
.
Напряженность Н (  ) в любой точке,
) в любой точке,
расположенной на сфере, создается массой
 части шара
части шара  , заключенной внутри
, заключенной внутри

 данной сферы
данной сферы  . (4.16)
. (4.16)
Поскольку масса
 V
V  , то
, то
Рис.4.2. 
 , (4.17)
, (4.17)
где  – плотность шара.
– плотность шара.
Как следует из (4.17), при постоянной плотности шара (  ) напряженность Н(
) напряженность Н( 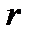 ) гравитационного поля внутри него возрастает линейно по мере перехода от центра шара к его поверхности.
) гравитационного поля внутри него возрастает линейно по мере перехода от центра шара к его поверхности.
Если теперь выразить плотность  шара через его радиус
шара через его радиус 
 V
V  , то получим
, то получим
 . (4.18)
. (4.18)
По данной формуле рассчитывается напряженность внутри любого однородного шара, в том числе и Земли (если считать массу равномерно распределенной по ее объему)  . (4.19)
. (4.19)
 ~ ~ 
|

|

|
 ~ ~ 
|
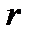 , отсчитываемого от центра Земли: для
, отсчитываемого от центра Земли: для  справедлива формула (4.19):
справедлива формула (4.19):  ; для
; для  выполняется формула
выполняется формула  .
.
r При рассмотрении других видов
полей мы увидим, что их
характеристики (напряженность,
Рис. 4.3. потенциал) будут определяться по
формулам, аналогичным (4.12) – (4.19).
5) сила тяжести является силой гравитационного, а вес тела – силой электромагнитного происхождения.
Дата добавления: 2014-10-31; просмотров: 257; Мы поможем в написании вашей работы!; Нарушение авторских прав |