Равномерное движение по окружности

( , но ; , , ).

В данном случае удобно перейти

к угловым величинам:

- угловое перемещение,

- угловая скорость,

0 - угловое ускорение.

На рис. 2.5 видно, что

, , (2.19)

Рис. 2.5. где 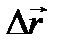- перемещение, 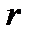- радиус окружности, и - радиус-векторы.

Угловой скоростью называют векторную физическую величину, характеризующую быстроту изменения углового перемещения:

. (2.20)

Аналогично, угловое ускорение . (2.21)

С помощью (2.19) можно найти связь между и с соответствующими линейными величинами и :

, , (2.22)

, . (2.23)

Поскольку и - величины векторные, направление которых находится по правилу правого винта, то налицо векторные произведения соответствующих векторов:

; . (2.24)

К вращательному движению применимы все формулы поступательного (прямолинейного) движения (см. (2.14) – (2.18)) при

Мощность N – скалярная физическая величина, характеризующая, быстроту (скорость) совершения работы:

при . (5.5)

Учтя (5.1), получим еще одно выражение для определения мощности: (5.6)

где - скорость перемещения тела. За единицу измерения работы в СИ принят джоуль: [А] = [F]·[ ]=Н·м = Дж. Единица измерения мощности - ватт: [N] = [A]/[t] = Дж/с = Bт.

Вcе силы, встречающиеся в макроскопической механике, подразделяются на консервативные (потенциальные) и неконсервативные.

Консервативными называются силы, работа которых зависит только от начального и конечного положений тела. Причем работа консервативной силы по произвольной замкнутой траектории (контуру) L равна нулю. Это следует из рассмотрения рис.5.3. изменение направления движения тела например,

в точке 2 вызывает изменение знака проекции консервативной

силы и знака её работы, то есть Рис. 5.3.

. Поэтому ,

или . (5.7)

В этой формуле знак указывает на то, что интегрирование проводится по замкнутому контуру L (см. также п. 4.1).

В качестве примера рассмотрим работу, совершаемую при перемещении тела в поле центральных сил (см. п. 4.2), например, в гравитационном поле. Докажем, что центральные силы консервативны, то есть , (5.8)

где учтено уравнение (4.2).

Действительно, так как , то , a (тело вышло из точки 1 и вернулось в эту же точку), то

Из (5.3) явствует, что сила не совершает работу в следующих случаях:

l) когда точка приложения силы неподвижна (тело покоится)

и r = const, a dr = 0;

2) если сила направлена по нормали к перемещению (угол ), например, центростремительная сила работы не совершает.

Работу производит лишь тангенциальная (касательная) составляющая силы. При этом, если < (см.рис. 5.1.а), то А > 0, если > (см.рис.5.1,б), то А < 0.

0

Рис. 5.1. б/

r

Рис. 5.2. Когда сила F постоянна на перемещении (рис. 5.2, a), то

. (5.4)

На рис.5.2,а видно, что работа постоянной силы соответствует площади прямоугольника со сторонами F_r и .

Если же сила различна в разных точках пути, то работа (см. рис. 5.2, б) численно равна площади криволинейной трапеции; аналитически она представляется формулой (5.3).

замене в них линейных величин на угловые (см. (2.19), (2.20), (2.21), (2.24)).

Период вращения Т – это время одного оборота (при этом ), где N – число оборотов.

Частота вращения – число оборотов в секунду: .

Учитывая эти определения, а также (2.21), получаем:

. (2.25)

Векторы , и направлены вдоль оси, перпендикулярной плоскости вращения и проходящей через центр окружности.

При ускоренном движении все эти три вектора сонаправлены; при замедленном (торможении) - имеет направление противоположное и .