Основные характеристики случайного спроса

Как и всякая другая случайная величина, спрос характеризуется своим ожидаемым (средним) значением, стандартным отклонением (характеристика разброса относительно среднего) и частотным распределением.

Среднее значение и стандартное отклонение спроса за принятый единичный период (день, неделя) должны быть определены по историческим данным о продажах данного товара, т.е. по числовой выборке.

Из числовой выборки желательно исключать любые катастрофические периоды (природные, финансовые, политические), любые периоды, содержащие мероприятия по продвижению данного товара и т.п., оставляя лишь «серые будни», ничем не отличающиеся друг от друга.

Пример такой выборки приведен на рисунке (Рис. 199). По вертикальной оси отложены количества проданного в разные дни товара (в стандартных контейнерах), а по горизонтальной – номер дня.

Рис. 199

Как видно из диаграммы (Рис. 199), несмотря на то, что в приведенном примере спрос весьма значительно варьирует день ото дня, в среднем он постоянен. Если провести по выбранной совокупности точек, так называемую, линию тренда, то она окажется почти горизонтальной. Линия тренда представляет собой меняющийся со временем центр числовой выборки. Обычно ее проводят, пользуясь принципом максимального правдоподобия, так, чтобы сумма квадратов отклонений точек выборки от линии тренда была минимальной.

Поскольку в рассматриваемом примере спрос в среднем не меняется со временем, его среднее значение можно найти простым усреднением всех точек выборки по формуле

где xi – спрос в i-ый день, N – количество дней в выборке, x – не меняющееся со временем среднее значение спроса за 1 день.

Очевидно, что одно только среднее значение недостаточно для характеристики случайного спроса. Необходимо также характеризовать величину разброса точек выборки вокруг среднего значения. Наиболее употребительной характеристикой разброса является среднеквадратичное или стандартное отклонение s. Эта величина определяется как корень квадратный из среднего значения квадрата отклонений ежедневного спроса от его среднего значения.

Среднее значение квадрата отклонений называется дисперсией s2.

Причина популярности именно этой характеристики разброса, а не, скажем, среднего значения модулей отклонений спроса от среднего, или максимальных отклонений от среднего и т.п., состоит в следующем. Если нас интересует суммарный спрос за L дней или суммарный спрос на один и тот же товар в L различных магазинах (обозначим его XL), иными словами, если мы изучаем случайный спрос, который можно представить как сумму случайных величин:

то оказывается, что среднее значение этого суммарного спроса равно

сумме средних значений каждого из случайных слагаемых, т.е. сумме средних

(ожидаемых) значений спроса каждый день, которые в случае в среднем

постоянного спроса одинаковы и равны , т.е.

Аналогично, дисперсия этого суммарного спроса равна сумме дисперсий каждого случайного слагаемого, которые в случае не меняющегося спроса то же одинаковы и равны дисперсии ежедневного спроса s²т.е.

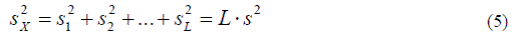
Тогда для стандартного отклонения суммарного спроса за L дней получим

Приведенные соотношения, представляют собой известные теоремы теории вероятности и отражают важнейшие закономерности случайности, проявляющиеся на практике. Если мы реально сделаем выборку значений суммарного спроса за L дней, оценим стандартное отклонение этого суммарного спроса и сравним его со стандартным отклонением спроса за 1 день, мы найдем, что стандартное отклонение выросло в раз, в то время как среднее значение суммарного спроса стало в L раз выше среднего значения дневного спроса. Таким образом, относительные вариации суммарного спроса за L дней в раз меньше, чем относительные вариации дневного спроса. Для характеристики относительных вариаций случайной величины используют коэффициент вариации:

Тогда можно написать, что коэффициент вариации суммарного спроса за

L дней в раз меньше, чем коэффициент вариации дневного спроса:

т.е. суммарный спрос за L дней в раз менее случаен, чем ежедневный спрос.

Подчеркнем еще раз, что при определении стандартного отклонения суммы случайных величин нельзя складывать стандартные отклонения каждой из них. Дело в том, что отклонения от среднего значения спроса одинаково часто и «с одинаковым размахом» происходят как вниз, так и вверх от него. Поэтому для суммы случайных величин они частично компенсируют друг друга. Закон, утверждающий, что складываются дисперсии этих величин (квадраты стандартных отклонений), количественно характеризует степень этой компенсации.

Заметим, что никакая другая характеристика разброса, кроме стандартного отклонения (корня из дисперсии), не позволяет выразить эти важнейшие статистические закономерности столь наглядно.

В случае, если числовая выборка значений спроса свидетельствует, что спрос непостоянен (см. Рис. 200), ожидаемая величина спроса, конечно, не может быть вычислена как простое среднее по выборке, по формуле

В этом случае с помощью специальных статистических методов прогноза нужно выделить линию тренда (в данном случае она включает линейный тренд с сезонными колебаниями) и продлить выделенные тенденции на некоторый промежуток времени в будущем.

Рис. 200

Разумеется, невозможно определить, как долго обнаруженная тенденция будет продолжаться. Однако если она существовала достаточно долго в прошлом, есть основания надеяться, что она сохранится и в ближайшем будущем.

Полученная линия тренда определяет ожидаемое (среднее) значение спроса в разные моменты времени в прошлом и в будущем . Кроме того, применяемый статистический метод прогноза обязательно выдаст стандартное отклонение точек выборки от линии тренда –s (поскольку сама линия проведена на основе минимизации s²).

Подчеркнем, что если все же вычислить ожидаемый спрос, как простое среднее, получится линия «прогноза», показанная пунктиром на Рис. 200.

Предсказываемое этой линией «ожидаемое» значение спроса не может иметь ничего общего с действительностью, но, что еще более важно, вычисленное на основе этого «ожидаемого» значения стандартное отклонение спроса

будет, очевидно, намного больше реального.