
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Доведення. Якщо , то маємо: , тобто при виконується
 .
.
Якщо  , то маємо:
, то маємо:  , тобто при
, тобто при  виконується
виконується  .
.
2)  .
.
Доведення. Покладемо  . Тоді
. Тоді  . Якщо
. Якщо  , то
, то  і
і 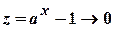 .
.
 .
.
Якщо  , то маємо:
, то маємо:  , тобто при
, тобто при  справедливо
справедливо  .
.
3)  .
.
Доведення. Покладемо  . Якщо
. Якщо  , то
, то  і
і  .
.
Далі 
 . Звідси маємо:
. Звідси маємо:  . Тоді
. Тоді

Розглянемо степенево-показниковий вираз  . Нехай
. Нехай 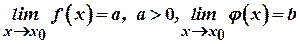 . Запишемо
. Запишемо
 .
.
Оскільки  , то
, то  . Звідси маємо
. Звідси маємо
 .
.
Зазначимо, що вирази 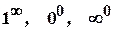 є не визначеними. Для знаходження відповіді на питання, що є границею виразу
є не визначеними. Для знаходження відповіді на питання, що є границею виразу  , у цих випадках недостатньо знати лише границі функцій
, у цих випадках недостатньо знати лише границі функцій  , потрібно знати закон, за яким вони прямують до своїх границь.
, потрібно знати закон, за яким вони прямують до своїх границь.
3. Класифікація точок розриву функції.
Точка називається точкою розриву функції , якщо функція у точці не є неперервною.
Точки розриву класифікують наступним чином.
Розриви першого роду. Якщо в точці функція має скінченну ліву й скінченну праву границю і вони рівні між собою, тобто
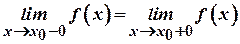 ,
,
Дата добавления: 2014-12-03; просмотров: 406; Мы поможем в написании вашей работы!; Нарушение авторских прав |