Нескінченно малі й нескінченно великі функції

Нескінченно малі функції. Функція називається нескінченно малою в точці ( або при ), якщо .

Аналогічно означаються нескінченно малі функції при .

Виходячи з означень границі функції за Гейне і за Коші, можна навести наступні рівносильні означення нескінченно малої функції.

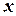Функція називається нескінченно малою в точці , якщо для будь-якої збіжної до послідовності значень аргументу , відмінних від , відповідна послідовність є нескінченно малою.

Функція називається нескінченно малою в точці , якщо для довільного числа 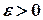існує число таке, що нерівність виконується для всіх 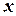, які задовольняють умову .

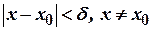Теорема . Число 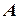є границею функції у точці тоді і тільки тоді, коли , де – нескінченно мала функція в точці .

Доведення. Нехай . Покажемо, що різниця є нескінченно малою в точці . Дійсно,

.

Нехай тепер , де – нескінченно мала функція в точці . Тоді

.

Нескінченно малі функції мають такі ж властивості, як і нескінченно малі послідовності:

алгебраїчна сума скінченного числа нескінченно малих у точці функцій є нескінченно малою в точці функцією;

добуток скінченного числа нескінченно малих у точці функцій, а також добуток нескінченно малої функції на обмежену функцію є нескінченно малою в точці функцією.

Викладене вище має місце також для нескінченно малих функцій функції при .

Нескінченно великі функції. Нехай функція визначена в деякому околі точки .

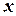Функція називається нескінченно великою в точці , якщо для будь-якого числа існує число таке, що для всіх , які задовольняють умову 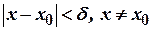, виконується нерівність .

Означення нескінченно великої в точці функції можна дати мовою послідовностей.

Функція називається нескінченно великою в точці , якщо для будь-якої збіжної до послідовності , відповідна послідовність значень функції є нескінченно великою.

Символічно це записують так: і говорять, що функція у точці має нескінченну границю.

Якщо при , то пишуть

.

Аналогічно означенням границі на нескінченності та скінченних односторонніх границь означаються нескінченні границі. При цьому використовуються відповідні записи, наприклад:

.

Теорема. Якщо нескінченно мала в точці функція, причому в околі точки , то функція у точці − нескінченно велика. І навпаки, якщо функція − нескінченно велика в точці , то функція у точці − нескінченно мала.

Дана теорема легко доводиться мовою послідовностей.