
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теореми про границі функцій
Теорема. Якщо функція  має границю в точці
має границю в точці  , то ця границя єдина.
, то ця границя єдина.
Доведення. Припустимо, що функція  має дві різні границі
має дві різні границі 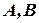 . Виберемо з області визначення функції
. Виберемо з області визначення функції  довільну послідовність
довільну послідовність  , збіжну до
, збіжну до  . Тоді послідовність
. Тоді послідовність  , згідно з означенням границі функції, матиме дві різні границі
, згідно з означенням границі функції, матиме дві різні границі 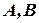 , що неможливо, оскільки будь-яка збіжна послідовність має єдину границю.
, що неможливо, оскільки будь-яка збіжна послідовність має єдину границю.
Теорема. Якщо функції  і
і 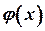 мають у точці
мають у точці  границі, то функції
границі, то функції  (при
(при  ) у точці
) у точці  також мають границі, причому
також мають границі, причому
 ; (3)
; (3)
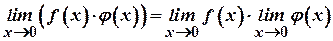 ; (4)
; (4)
 . (5)
. (5)
Доведення. Нехай послідовність 
 – довільна збіжна до
– довільна збіжна до  послідовність значень аргументу функцій
послідовність значень аргументу функцій  і
і 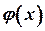 . Тоді відповідні послідовності
. Тоді відповідні послідовності  і
і 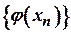 збіжні й за властивостями збіжних послідовностей
збіжні й за властивостями збіжних послідовностей
 ;
;
 ;
;
 (де
(де 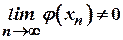 ).
).
Отже, згідно з означенням границі функції мають місце співвідношення 3-5.
Теорема . Нехай функції  і
і 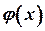 , визначені в деякому околі точки
, визначені в деякому околі точки  , крім, можливо, самої точки
, крім, можливо, самої точки  , мають у точці
, мають у точці  границі, й такі, що в околі точки
границі, й такі, що в околі точки 
 . Тоді
. Тоді  .
.
Доведення. Виберемо в околі точки  довільну збіжну до
довільну збіжну до  послідовність
послідовність 
 . Тоді послідовності
. Тоді послідовності  і
і 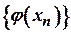 збіжні й
збіжні й  . Тому за відповідною властивістю збіжних послідовностей
. Тому за відповідною властивістю збіжних послідовностей  .
.
Звідси, за означенням границі функції в точці,  .
.
Наслідок. Якщо в деякому околі  , крім, можливо, самої точки
, крім, можливо, самої точки  , виконується нерівність
, виконується нерівність  і функція
і функція  у точці
у точці  має границю, то
має границю, то  .
.
Теорема 3.5. Нехай функції  визначені в деякому околі точки
визначені в деякому околі точки  , крім, можливо, самої точки
, крім, можливо, самої точки  , функції
, функції  мають у точці
мають у точці  границю, рівну
границю, рівну 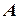 , тобто
, тобто 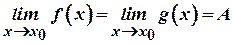 . Нехай, крім того, виконується нерівність
. Нехай, крім того, виконується нерівність 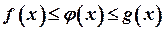 . Тоді функція
. Тоді функція 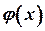 у точці
у точці  має границю, рівну
має границю, рівну 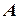 , тобто
, тобто 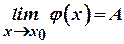 .
.
Доведення. Нехай 
 – довільна збіжна до
– довільна збіжна до  послідовність. Послідовності
послідовність. Послідовності  і
і 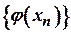 відповідних значень функції
відповідних значень функції  збіжні, й
збіжні, й  . Оскільки
. Оскільки 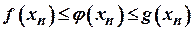 , то згідно з відповідною властивістю збіжних послідовностей
, то згідно з відповідною властивістю збіжних послідовностей  . Отже, за означенням границі функції в точці
. Отже, за означенням границі функції в точці 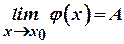 .
.
Зауваження. Наведені вище теореми про границі мають місце і для випадків  .
.
ЛЕКЦІЯ 11
24. Визначні границі.
25. Нескінченно малі й нескінченно великі функції.
26. Порівняння нескінченно малих функцій. Еквівалентні нескінченно малі функції.
Дата добавления: 2014-12-03; просмотров: 540; Мы поможем в написании вашей работы!; Нарушение авторских прав |