Визначні границі

.

Розглянемо у крузі радіуса гострий кут , хорду 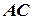і дотичну до кола в точці (рис. 4). Для площ трикутників та колового сектора виконуються нерівності

.

Отже,

.

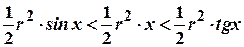Звідси

.

Розділивши ці нерівності на ( , оскільки ), одержимо . Із останніх нерівностей випливає

.

Помноживши всі частини на (–1) та додавши 1, матимемо

.

Оскільки , то .

Задамо довільне число 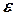> 0. Нерівність

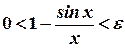або

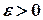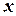справджується, як тільки , тобто . Таким чином, для довільного числа існує число таке, що для всіх , які задовольняють умову , виконується нерівність

.

Із цього випливає, що 1 є правою границею функції , тобто 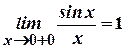. Оскільки функція парна, то і . Отже, .

Друга визначна границя. Доведемо, що

.

Раніше було встановлено, що . Нехай . Покладемо . Тоді , де 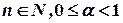. Оскільки , то . Отже,

. (6)

Якщо , то і . При цьому

Ураховуючи співвідношення (6), маємо

.

Нехай тепер . Покладемо . Тоді

Ураховуючи обидва випадки, одержуємо

.