Приклад. Теорема. Для того, щоб функції

При маємо отже,

Теорема. Для того, щоб функції і були еквівалентними нескінченно малими в околі точки , необхідно й достатньо, щоб їх різниця була в околі точки нескінченно малою вищого порядку по відношенню до кожної з функцій та .

Доведення. Нехай в околі точки . Тоді

Отже, необхідність доведено. Доведемо достатність.

Нехай .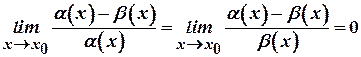

Звідси маємо

.

Таким чином, , тобто в околі точки .

ТЕМА 4. НЕПЕРЕРВНІ ТА РІВНОМІРНО НЕПЕРЕРВНІ ФУНКЦІЇ

ЛЕКЦІЯ 12

27. Неперервність функції в точці.

28. Операції над неперервними функціями.

29. Класифікація точок розриву функції.

1. Неперервність функції в точці

Нехай функція визначена в деякому околі точки .

Функція називається неперервною в точці , якщо .

Наведемо означення неперервності функції, які ґрунтуються на означеннях границі функції за Гейне і за Коші.