Операції над неперервними функціями

Доведення цієї теореми безпосередньо випливає з означення неперервності функції в точці та властивостей границь.

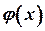Теорема (про неперервність складеної функції). Якщо функція неперервна в точці , а функція неперервна в точці 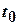, причому , то складена функція неперервна, як функція від , у точці .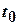

Доведення. Нехай задано довільне число 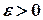. Тоді за неперервністю функції у точці знайдеться число 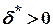таке, що для всіх 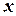, які задовольняють умову .

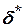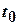Для числа за неперервністю функції у точці знайдеться число таке, що 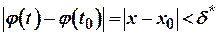для всіх , які задовольняють умову .

Отже, для довільного числа 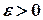знайдеться число таке, що з умови випливає нерівність , а це означає, що функція неперервна в точці .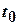

Можна довести, що всі елементарні функції в області їх визначення неперервні.

Звернемо увагу на те, що з означення неперервності функції у точці випливає