Элементы теории корреляции.

Основные понятия

Зависимость величины y или х называют функциональной, если каждому значению х отвечает единственное значение величины y. Если х – детерминированная величина, то есть принимающая целиком определенное значение, то и y есть детерминированная, если же х – случайная величина, то и y также случайная величина.

Однако же, чаще в окружающем нас мире имеет место не функциональная, а стохастическая, или вероятностная зависимость, когда каждому фиксированному значению независимой переменной х соответствует не одно, а множество значений переменных у, причем сказать заранее, какое именно значение примет величина у, невозможно.

Предположим, что существует стохастическая зависимость случайной переменной y от х. Присвоим некоторое значение х переменной Х. При переменная y в силу ее стохастической зависимости от х может принять любое значение из некоторого множества, причем какое именно, заранее неизвестно.

Среднее этого множества называют групповымгенеральным средним переменной Y при Х = х , или математическим ожиданием случайной величины Y, вычисленной при условии, что Х = х, это условное математическое ожидание обозначают как .

Если существует стохастическая зависимость Y от Х, то прежде всего стараются выяснить, меняются или нет при изменению Х условные математические ожидания .

Статистической называют зависимость, при которой изменение одной из величин влечет изменение распределения другой.

В частности, статистическая зависимость проявляется в том, что при изменении одной из величин меняется среднее значение другой; в этом случае статистическую зависимость называют корреляционной.

Говорят, что имеет место корреляционная зависимость Y от Х, если при изменению Х меняются условные математические ожидания , если же условные математические ожидания остаются неизменными, то говорят, что корреляционная зависимость Y от Х отсутствует.

Функция , которая описывает изменение условного математического ожидания случайной переменной Y при изменению значений х переменной Х, называется функцией регрессии.

Условным средним называют среднее арифметическое значений , которые наблюдались при соответствующих .

Например, если при величина приняла значение , то условное среднее .

Условным средним называют среднее арифметическое значений 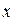, которые наблюдались при соответствующих .

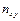При большом количестве наблюдений одно и то значение может встретиться раз, одно и то значение – раз, одна и та же пара чисел может встретится раз. Поэтому данные наблюдений группируют, подсчитывая частоты , , 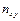. Все сгруппированные данные записывают в виде таблицы, которую называют корреляционной, например:

у	х
0-20	20-40	40-60	60-80
9-11
11-13
13-15
15-17
17-19
19-21