Обработка выборки методом наименьших квадратов

Оценка параметров линейной функции

При экспериментальном изучении функциональной зависимости одной величины Y от другой величины Х делают ряд измерений величины у при разных значениях х. Результаты могут быть представлены в виде таблицы:

			…		…
			…		…

Метод, основанный на требовании минимизации суммы квадратов отклонений, называется методом наименьших квадратов.

С его помощью изображают статистическую функциональную зависимость в виде аналитической зависимости и выражаются такие оценки параметров уравнения регрессии, которые сводят к минимуму избранную меру разброса.

В результате происходит выравнивание эмпирических значений в одну линию регрессии.

При этом, для однозначного определения как меру разброса используют один из показателей рассеивания случайной величины – дисперсию.

Предположим, что диаграмма рассеивания такова, что между величинами х и у существует линейная зависимость

,

где параметры а и – неизвестные.

Это означает, что отклонение фактических значений функции от «подобранной прямой» должны быть минимальными, то есть прямая подбирается так, чтобы сумма квадратов отклонений была минимальной

.

Пусть – есть уравнения « подобранной прямой».

Тогда должна выполняться равенство

.

Нужно определить параметры а и b так, чтобы z достигло минимума.

Известно, что необходимое условие существования минимума заключается в том, что:

После дифференцирования и упрощений, получим систему уравнений

которая называется системой нормальных уравнений в случае выбора эмпирической функции в виде линейной зависимости.

Пример 1. Методом наименьших квадратов найти значение параметров эмпирической функции, если исследовательские данные о значениях х и у представленные в таблице:

Решение. 1. По выборке наблюдений построим в системе координат х0у диаграмму рассеивания, то есть построим точки

.

2. Анализ исследовательских данных показывает, что в качестве эмпирической (подобранной) функции можно использовать линейную функцию

.

Для нахождения параметров а и b применим МНК.

Тогда для определения параметров а и b необходимо решить систему нормальных уравнений:

3. Для удобства вычислений составим следующую расчетную таблицу ( ):

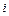
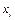
Подставим данные последней строки таблицы в нормальную систему уравнений:

Решив систему, получим

.

Подставляя эти значения параметров, получим эмпирическую функцию:

,

которая описывает зависимость между случайными величинами х и у.

2.8 Индивидуальное семестровое задание №2 «Метод наименьших квадратов»

По предоставленным статистическим данным подобрать эмпирическую функцию, и:

1. построить диаграмму рассеивания,

2. записать эмпирическую функцию,

3. записать систему нормальных уравнений,

4. составить расчетную таблицу,

5. решить полученную систему и записать эмпирическую функцию с найденными параметрами.

Считая, что зависимость между переменными и имеет вид 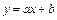, найти оценки параметров для следующих виборок:

1)

2)

3)

4)

		4 1
	6,3	6,0	7,5	8,5	3,5	6,2	7,5	8,7	6,0	3,7

5)

6)

7)

8)

	6,0	6,1	6,8	7,2	7,4	7,9	8,2	8,5	8,6	9,1

9)

10)

		8,5	9,2	9,6	9,4	10,5	11,2	10,8	11,0	11,5

11)

	2,5	3,1	3,0	3,5	4,2	5,1	5,5	6,0	6,2	6,4

12)

13)

14)

	66,7	71,0	76,3	80,6	85,7	92,9	99,4	113,6	125,1

15)

	0,30	0,91	1,50	2,00	2,20	2,62	3,00	3,30
	0,20	0,43	0,35	0,52	0,81	0,68	1,15	0,85

16)

17)

	7,6	7,2	6,2	8,3	8,2	7,6	7,9	7,5	8,5	8,7	7,0	8,8	8,5

18)

19)

20)

	14,39	9,45	7,05	5,32	16,94	1,97	8,75	3,41	13,37	8,22	9,39

21)

	2,7	4,6	6,3	7,8	9,2	10,6	12,0	13,4	14,7
	17,0	16,2	13,3	13,0	9,7	9,9	6,2	5,8	5,7

22)

	7,9	11,6	12,8	14,9	16,3	18,6	20,3	21,9	23,6
	13.0	22,8	24,8	28,6	31,6	38,7	40,0	44,9	43,0

23)

	0,21	0,32	0,58	1,02	1,76	2,68	3,75	5,07	6,62	8,32	10,21	12,33

24)

			б
	4,5			7,5