Решение. 1. Перейдем к дискретным распределениям, то есть за значения переменных X и примем середины соответствующих интервалов.

1. Перейдем к дискретным распределениям, то есть за значения переменных X и примем середины соответствующих интервалов.

Для вычисления выборочного коэффициента корреляции необходимо вычислить выражение , для чего составим корреляционную таблицу в условных вариантах.

За условный нуль взята варианта х = 60, а за условный нуль взята варианта у = 25, которые расположены приблизительно в

серединах соответствующих вариационных рядов.

2. В каждой клетке, в которой частота , записываем в правом верхнем углу произведение частоты 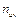на варианту и .

3. Находим сумму всех чисел, которые стоят в правых верхних углах клеток одной строки и записываем ее в клетку столбца и .

4. Умножим варианту v на u и полученное произведение записываем в последнюю клетку той же строки.

5. С целью контроля аналогичные вычисления проводим в столбце, причем произведения записываем в левом нижнем углу каждой клетки, для которых , после чего их прибавляем и полученную сумму записываем в строку V.

Потом умножаем варианту и на v и результат записываем в последней строке.

	-2	-1
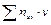
-2							-20
-1							-21
							-2
	-17	-27	-7

6. Вычисляем и :

.

.

7. Вычисляем вспомогательные величины и :

.

.

8. Вычислим и :

.

.

9. Искомый выборочный коэффициент корреляции:

.

Так как > 0, эта связь прямая.

10. Выборочное уравнение прямой линии регрессии Y на Х имеет вид:

Вычислим ( 0, , , ):

.

.

.

11. Уравнение прямой линии регрессии на X:

.

.

.

.

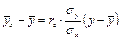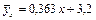12. Уравнение прямой линии регрессии X на :

.

.

.

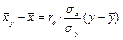13. По соответствующему уравнению регрессии оценим средний вес семян тех растений, вес которых равен 60 г, и сравним его с соответствующим групповым средним.

.

.

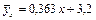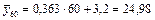Если воспользоваться непосредственно таблицей, то

.

Как видим, согласование расчетного и наблюдаемого условных средних – удовлетворительное.

2.10. Индивидуальное семестровое задание №3 “Нахождение выборочного коэффициента корреляции и прямых линий регрессии”

В каждом варианте предоставлена таблица, которая определяет некоторое непрерывное распределение. По этому распределению необходимо составить дискретное распределение, взяв за значения и середины соответствующих интервалов и предполагая, что между и существует линейная корреляционная зависимость, выполнить такую работу:

1. Вычислить коэффициент корреляции и проанализировать направление связи между и .

2. Составить уравнения прямых регрессии на и на .

3. Вычислить для данного значения одной переменной соответствующее значение другой, использовав для этого одно из полученных уравнений регрессии (подходящее) и сравнить это значение с соответствующим групповым средним.

Вариант 1. При обследовании 100 учеников получены такие данные об их росте (см) и весе (кг):

	х
117,5-122,5	122,5-127,5	127,5-132,5	132,5-137,5	137,5-142,5	142,5-147,5
32-36
36-40
40-44
44-48
48-52

По соответствующему уравнению регрессии оценить средний вес учеников, рост которых равен 135 см, и сравнить его с соответствующим групповым средним.

Вариант 2. Распределение 160 работниц по количеству обслуживаемых станков (шт.) и почасовой выработки ткани (м) представлено в таблице:

	х
10-15	15-20	20-25	25-30	30-35	35-40	40-45
5-7
7-9
9-11
11-13
13-15
15-17
17-19

По соответствующему уравнению регрессии оценить среднюю почасовую выработку работниц, которые обслуживают 10 станков и сравнить ее с соответствующим групповым средним.

Вариант 3. Распределение 50 магазинов по размеру товарооборота (млн. гр) и величиной торговой площади ( м ²) представлено в таблице:

	х
100-150	150-200	200-250	250-300	300-350
1,0-1,5
1,5-2,0
2,0-2,5
2,5-3,0

По соответствующему уравнению регрессии оценить средний товарооборот тех магазинов, размер торговой площади которых составляет 225 м ², и сравнить его с соответствующим групповым средним.

Вариант 4. Распределение 100 изделий по стоимости готового изделия (грн) и стоимостью сырья (грн) представлено в таблице:

	х
5-15	15-25	25-35	35-45	45-55
0,5-5,5
5,5-10,5
10,5-15,5
15,5-20,5
20,5-25,5
25,5-30,5

По соответствующему уравнению регрессии оценить среднюю стоимость готового изделия, стоимость сырья которого составляет 30 грн., и сравнить его с соответствующим групповым средним.

Вариант 5. Распределение 50 предприятий по стоимости основных производственных фондов (млн. грн) и затратами (% к стоимости основных фондов) на капитальный ремонт представлен в таблице:

у	х
1-3	3-5	5-7	7-9	9-11	11-13	13-15
5-9
9-13
1-17
17-21
21-25
25-29

По соответствующему уравнению регрессии оценить средние затраты на капитальный ремонт предприятия, стоимость основных производственных фондов которого равна 12 млн. грн, и сравнить их с соответствующим групповым средним.

Вариант 6. Распределение 40 заводов цветной металлургии по среднесуточному изготовлению металла (тыс.т) и затратами электроэнергии на 1 тн. (тыс. квт-час) представлено в таблице:

	х
10-15	15-20	20-25	25-30	30-35
2,0-2,5
2,5-3,0
3,0-3,5
3,5-4,0
4,0-4,5

По соответствующему уравнению регрессии оценить средние затраты электроэнергии на 1 тн. металла тех заводов, у которых среднесуточное изготовление металла составляет 22,5 тыс.т., и сравнить их с соответствующим групповым средним.

Вариант 7. Распределение 80 коров по живому весу (кг) и надоями молока (кг) представлено в таблице:

	Х
325-375	375-425	425-475	475-525	525-575
1250-1750
1750-2250
2250-2750
2750-3250
3250-3750

По соответствующему уравнению регрессии оценить средний надой молока у коров, живой вес которых составляет 400 кг, и сравнить его с соответствующим групповым средним.

Вариант 8. Распределение 100 ткацких фабрик по производственным мощностям (тыс. г. за час) и себестоимостью 1 м ткани (грн) представлено в таблице:

	Х
0-100	100-200	200-300	300-400	400-500
7,75-8,25
8,25-8,75
8,75-9,25
9,25-9,75
9,75-1025

По соответствующему уравнению регрессии оценить среднюю себестоимость 1 м ткани тех фабрик, производственные мощности которых составляют 250 тыс. г. на год, и сравнить ее с соответствующим групповым средним.

Вариант 9. Распределение 100 прямоугольных чугунных плиток по длинне (см) и массе (кг) представлено в таблице:

	х
15-25	25-35	35-45	45-55	55-65	65-75	75-85
9-15
15-21
21-27
27-33
33-39
39-45

По соответствующему уравнению регрессии оценить среднюю массу тех плиток, длина которых составляет 50 см, и сравнить ее с соответствующим групповым средним.

Вариант 10. Распределение 200 заводов по стоимости основных фондов (млн. грн.) и стоимостью готовой продукции ( млн. грн.) представлено в таблице:

	х
10-20	20-30	30-40	40-50	50-60
15-25
25-35
35-45
45-55
55-65

По соответствующему уравнению регрессии оценить среднюю стоимость готовой продукции тех заводов, стоимость основных фондов которых составляет 35 млн. грн., и сравнить ее с результатом, полученным непосредственно из таблицы

Вариант 11. Распределение предприятий по объему продукции (грн) и ее себестоимостью (грн) предоставлено в таблице:

у	х
500-1500	1500-2500	2500-3500	3500-4500	4500-5500
1,75-2,25
2,25-2,75
2,75-3,25
3,25-3,75
3,75-4,25

По соответствующему уравнению регрессии оценить среднюю себестоимость продукции тех предприятий, объем продукции которых составляет 3000 грн, и сравнить ее с соответствующим групповым средним.

Вариант 12. Распределение 120 вагонных колес по сроку службы ( в годах) и величиной износа обода колеса (в мм) представлено в таблице:

	х
0,5-1,5	1,5-2,5	2,5-3,5	3,5-4,5	4,5-5,5	5,5-6,5	6,5-7,5
2,5-7,5
7,5-12,5
12,5-17,5
17,5-22,5
22,5-27,5

По соответствующему уравнению регрессии оценить среднее значение износа вагонного колеса, срок службы которого равна 4 годам, и сравнить его с соответствующим групповым средним.

Вариант 13. Распределение 200 растений по общему весу всего растения (г) и весу семян (г) представлено в таблице:

	х
35-45	45-55	55-65	65-75	75-85
12,5-17,5
17,5-22,5
22,5-27,5
27,5-32,5
32,5-37,5

По соответствующему уравнению регрессии оценить средний вес семян тех растений, вес которых равна 60 г, и сравнить ее с соответствующим групповым средним.

Вариант 14. Распределение 100 проб руды с содержимым окиси железа (%) и закиси железа (%) представлено в таблице:

	х
20-30	30-40	40-50	50-60	60-70	70-80	80-90
0-6
6-12
12-18
18-24
24-30
30-36

По соответствующему уравнению регрессии оценить средний процент закиси железа тех проб руды, содержимое окиси железа которых составляет 65%, и сравнить его с соответствующим групповым средним.

Вариант 15. Распределение однотипных предприятий по стоимости основных фондов (млн. грн) и себестоимостью единицы продукции (грн) представлено в таблице:

	х
5,5-10,5	10,5-15,5	15,5-20,5	20,5-25,5	25,5-30,5
1,125-1,375
1,375-1,625
1,625-1,875
1,875-2,125
2,125-2,375

По соответствующему уравнению регрессии оценить среднее значение себестоимости единицы продукции тех предприятий, стоимость основных фондов которых составляет 18 млн. грн., и сравнить его с соответствующим групповым средним.

Вариант 16. Распределение 100 прямоугольных плиток по их длине (см) и массе (кг) представлено в таблице:

	х
27,5-32,5	32,5-37,5	37,5-42,5	42,5-47,5	47,5-52,5
5-7
7-9
9-11
11-13
13-15

По соответствующему уравнению регрессии оценить среднюю массу плиток, длина которых равна 40 см, и сравнить ее с соответствующим групповым средним.

Вариант 17. Данные о стоимости годового ремонта (в тыс. грн.) 50 однотипных станков и продолжительностью их эксплуатации ( в годах) содержит таблица:

	х
1-3	3-5	5-7	7-9	9-11
0,5-1,5
1,5-2,5
2,5-3,5
3,5-4,5
4,5-5,5

По соответствующему уравнению регрессии оценить среднюю стоимость годового ремонта тех станков, продолжительность эксплуатации которых равна 8 годам, и сравнить ее с соответствующим групповым средним.

Вариант 18. Результаты обследования роста (см) 50 учеников и их весы (кг) представлено в таблице:

	х
117,5-122,5	122,5-127,5	127,5-132,5	132,5-137,5	137,5-142,5	142,5-147,5	147,5-152,5
22,5-25,5
25,5-28,5
28,5-31,5
31,5-34,5
34,5-37,5

По соответствующему уравнению регрессии оценить средний вес учеников, рост которых равна 135 см, и сравнить ее с соответствующим групповым средним.

Вариант 19. Распределение 40 предприятий региона по количеству ремонтных слесарей (ед) и числу станкосмен (тис. ед) содержит таблица:

	х
0-0,2	0,2-0,4	0,4-0,6	0,6-08	0,8-1,0	1,0-1,2
10-15
15-20
20-25
25-30
30-35
35-40

По соответствующему уравнению регрессии оценить среднее количество слесарей тех предприятий, рост число станкосмен которых составляет 0,3 тыс. ед., и сравнить ее с соответствующим групповым средним.

Вариант 20. Распределение 50 шахт области по уровню газоносности угольных пластов ( м ³/т) и себестоимостью угля (грн/т) представлено в таблице:

	х
0-8	8-18	16-24	24-32	32-40
80-90
90-100
100-110
110-120
120-130

По соответствующему уравнению регрессии оценить среднее значение себестоимости угля тех шахт, газоносность угольных пластов которых составляет 28 м ³/т , и сравнить полученный результат с соответствующим групповым средним.

Вариант 21. Распределение 40 шахт некоторого района по уровню газоносности угольных пластов ( м ³/т) и объемом суточной добычи (т) представлено в таблице:

	х
0-10	10-20	20-30	30-40	40-50
650-750
750-850
850-950
950-1050
1050-1150

По соответствующему уравнению регрессии оценить среднее значение себестоимости угля тех шахт, глубина выработок которых составляет 28 м ³/т, и сравнить результат с соответствующим групповым средним.

Вариант 22. Распределение 40 шахт некоторого района по глубине выработок (м) и себестоимостью угля (грн./т) представлено в таблице:

	х
550-650	650-750	750-850	850-950	950-1050
80-90
90-100
100-110
110-120
120-130

По соответствующему уравнению регрессии оценить среднее значение себестоимости угля тех шахт, глубина выработок которых составляет 800 м, и сравнить полученный результат с соответствующим групповым средним.

Вариант 23. Распределение 100 проб стали по содержимому углерода (%) и твердостью (НВ) представлено в таблице:

	х
0,1-0,2	0,2-0,3	0,3-0,4	0,4-0,5	0,5-06	0,6-0,7	0,7-0,8
130-150
150-170
170-190
190-210
210-230
230-250

По соответствующему уравнению регрессии оценить среднее значение тех проб стали, содержимое углерода в которых составляет 0,55%, и сравнить полученный результат с соответствующим групповым средним.

Вариант 24. Распределение 100 проб стали по содержимому углерода (%) и временном сопротивлением (Н/мм²) представлено в таблице:

	х
0,1-0,25	0,25-0,4	0,4-0,55	0,55-07	0,7-0,85
40-50
50-60
60-70
70-80
80-90

По соответствующему уравнению регрессии оценить среднее значение временного сопротивления тех проб стали, содержимое углерода в которых составляет 0,475%, и сравнить полученный результат с соответствующим групповым средним.

Вариант 25. Распределение 40 шахт некоторого района по глубине виработок (м) и газоносностью ( м ³/т) угольных пластов даны в таблице:

	х
750-850	850-950	950-1050	1050-1150	1150-1250
5-15
15-25
25-35
35-45

По соответствующему уравнению регрессии оценить среднее значение газоносности тех шахт, глубина выработок которых составляет 900 м, и сравнить его с соответствующим групповым средним.