Линейная корреляция

Если обе линии регрессии на и на – прямые, то корреляция называется линейной.

Для оценки силы линейной корреляционной связи служит выборочный коэффициент корреляции .

Выборочный коэффициент корреляции определяется равенством

,

где: – варианты признаков Х и Y ;

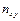– частота пары ;

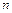– объем выборки;

– выборочные средние квадратические отклонения;

– выборочные средние признаков Х и Y.

Если перейти к условным вариантам

,

то этот выборочный коэффициент корреляции вычисляется по формуле

.

Уравнение прямых регрессии Y на Х и Х на Y имеют вид

,

.

где – условные средние, то есть средние значения одной переменной, которые отвечают определенному значению другой.

Пример 1.Распределение 195 растений по общему весу всего растения Х (г) и весу семян Y (г) представлено в таблице:

35-45	45-55	55-65	65-75	75-85
12,5-17,5
17,5-22,5
22,5-27,5
27,5-32,5
32,5-37,5

По соответствующему уравнению регрессии оценить средний вес семян тех растений, вес которых равен 60 г, и сравнить его с соответствующим групповым средним.

Допуская, что между Х и существует линейная корреляционная зависимость:

1. Вычислить коэффициент корреляции и проанализировать направление связи между Х и .

2. Составить уравнение прямых регрессии на X и Х на .

3. По соответствующему уравнению регрессии оценить средний вес семян тех растений, вес которых равна 60 г, и сравнить ее с соответствующим групповым средним.