
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема 8. Индексный метод
Цель занятия: Ознакомится с различными видами индексов, их применением и расчетом.
Индивидуальные индексы:  - физического объема;
- физического объема;  - цен.
- цен.
8.1 Агрегатные индексы. Модель задачи: Д = ∑ qi · pi.
Относительное изменение объемного показателя.
Индекс стоимости продукции (услуг, товарооборота): Iq,p  *100,%;
*100,%;
Агрегатный индекс цен: Ip=  *100,%; индекс цен Паше
*100,%; индекс цен Паше
Ip=  *100,%; индекс цен Ласпейреса
*100,%; индекс цен Ласпейреса
Общий индекс физического объема услуг:  *100,%.
*100,%.
Индекс стоимости услуг равен произведению индекса физического объема услуг и индекса цен:  .
.
Абсолютное изменение объемного показателя.


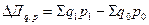
Задача 8.1. Провести факторный анализ динамики доходов от услуг связи в относительном и абсолютном измерении, используя индексный метод. Сделать выводы по результатам.
Исходные данные Таблица 8.1
| Виды услуг | Средний тариф, руб. | Количество услуг, тыс. ед. | ||
| Базисный год | Отчетный год | Базисный год | Отчетный год | |
| посылки | ||||
| письма | ||||
| переводы |
Расчетная таблица Таблица 8.2
| Виды Услуг | Средний тариф руб. | Количество услуг тыс. единиц | Доходы, тыс.руб. | ||||
| Базисный год (0) | Отчетный год (1) | Базисный год (0) | Отчетный год (1) | Базисный год р0q0 | Отчетный год р1q1 | Условные р0q1 | |
| посылки | |||||||
| письма | |||||||
| переводы | |||||||
Относительное изменение объемного показателя:
Iv = 10316*100/6892 = 149,68% Ip = 10316*100/7303 = 141,26% Iq = 7303*100/6892 = 105,96%
1,4126*1,0596 = 1,4968
Абсолютное изменение объемного показателя:
∆Дv = 10316 – 6892 = 3424 тыс.руб. ∆Дp = 10316 – 7303 = 3013 тыс.руб.
∆Дq = 7303 – 6892 = 411 тыс.руб.
Доля прироста доходов за счёт роста среднего тарифа:
 = 0,880 или 88,0 %.
= 0,880 или 88,0 %.
Доля прироста доходов за счёт роста количества услуг:
 = 100-88,0 = 12 %.
= 100-88,0 = 12 %.
Вывод: доходы от услуг связи в отчетном году выросли на 49,68% или на 3424 тыс.руб.
в том числе за счет роста среднего тарифа они выросли на 41,26% или на 3013 тыс.руб., а за счет роста количество услуг они выросли только на 5,96% или на 411 тыс.руб.
В основном рост доходов произошел за счет роста среднего тарифа – 88 %.
8.2 Среднеарифметический и среднегармонический индексы.
Агрегатный индекс нельзя исчислить, если один из показателей задан в виде индивидуального индекса ( 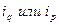 ). Тогда его заменяет средний индекс, тождественный агрегатному.
). Тогда его заменяет средний индекс, тождественный агрегатному.
Индекс физического объема услуг может быть преобразован в средний арифметический индекс: Iq  ;
;  , отсюда q1 = iq∙q0.
, отсюда q1 = iq∙q0.
Агрегатный индекс цен может быть преобразован в средний гармонический индекс:  . Ip = p1/p0, отсюда p0 = p1/iр;
. Ip = p1/p0, отсюда p0 = p1/iр;
Задача 8.2 По данным предприятия связи о доходах в базисном году и индексах изменения физического объема в отчетном году рассчитать средний индекс изменения объема услуг.
Исходные данные Таблица 7.3
| Виды доходов от предоставления услуг | Доходы в базисном году, млн. руб. | Изменение физического объема услуг в отчетном году, % |
| Почтовой связи | - 6,4 | |
| Телефонной связи | + 8,2 | |
| Телеграфной связи | - 2,5 |
Используется среднеарифметический индекс физического объема: 
Расчетная таблица Таблица 7.4
| Доходы в базисном году, млн. руб | Изменение физического объема услуг в отчетном году, %
 ,% ,% 
| Доходы в отчетном году

|
| - 6,4 -0,064 0,936 | ||
| + 8,2 +0,082 1,082 | ||
| - 2,5 -0,025 0,975 | 916,5 | |
| + 2,9 | 5485,5 |
Средний индекс изменения объема услуг: 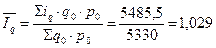 или 102,9 %
или 102,9 %
Средний индекс прироста объема услуг: 102,9 -100 = 2,9 %.
Задача 8.3 По данным предприятия связи о доходах в текущем году и индексах изменения цен в текущем году по сравнению с базисным рассчитать средний индекс изменения цен.
Исходные данные Таблица 8.5
| Виды доходов от предоставления услуг | Доходы в текущем году, млн. руб. | Изменение цен в текущем году, % |
| Почтовой связи | + 3,6 | |
| Телефонной связи | + 5,8 | |
| Телеграфной связи | + 2,5 |
Используется среднегармонический индекс цен: 
Расчетная таблица Таблица 8.6
| Доходы в текущем году, млн. руб | Изменение цен в текущем году, %
 ,% ,% 
| Доходы в отчетном году

|
| + 3,6 +0,036 1,036 | ||
| + 5,8 +0,058 1,058 | ||
| + 2,5 +0,025 1,025 | ||
| + 4,7 |
Средний индекс изменения цен:  или 104,7 %.
или 104,7 %.
Средний индекс прироста цен: 104,7 -100 = 4,7 %.
Среднегармонический индекс себестоимости: 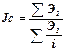
Общая экономия затрат: 
Среднеарифметический индекс производительности труда: 
Общая экономия рабочей силы: ΔT = ΣiT1 - ΣT1 = Т1*(Iпер-1).
Задача 8.4 По данным предприятия связи о среднесписочной численности работников, затратах, приросте производительности труда в отчетном периоде по сравнению с базисным и индексах себестоимости рассчитать общие индексы производительности труда и себестоимости услуг, а также общую экономию рабочей силы в связи с ростом производительности труда.
Исходные данные Таблица 7.7
| № цеха | Ср.списочная численность работников в отчетном периоде, чел. | Затраты в отчетном периоде, млн. руб. | Прирост производительности труда в отчетном периоде по сравнению с базисным, % | индекс себестоимости услуг |
| 0,9 | ||||
| 0,85 | ||||
| 0,95 |
Расчетная таблица Таблица 7.8
| № цеха | Тi | Эi | ∆Iw Iw | 
|
| 4 1,04 | 0,90 | |||
| 5 1,05 | 0,85 | |||
| 10 1,10 | 0,95 | |||
| 5,9 | 0,895 |
Используется гармонический индекс себестоимости:
 или 89,5 %.
или 89,5 %.
Общая экономия затрат:  млн. руб.
млн. руб.
Используется среднеарифметический индекс производительности труда:
 или 105,9 %,
или 105,9 %,
прирост составит: 105,9 - 100 = 5,9 %.
Общая экономия рабочей силы: ΔT = ΣiT1 - ΣT1 = 1091 – 1030 = 61 шт. ед.
8.3. Индексы качественных показателей.
Модель задачи: 
Дата добавления: 2014-12-23; просмотров: 293; Мы поможем в написании вашей работы!; Нарушение авторских прав |