
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Корреляционно-регрессионный анализ для многофакторной модели.
Задача 5.3 По данным о доходах основной деятельности, внереализационных доходов и прибыли (млрд. руб.) построить уравнение связи, измерить тесноту связи между прибылью и доходами, провести полный корреляционно- регрессионный анализ связи.
Исходные данные и расчеты Таблица 6.3
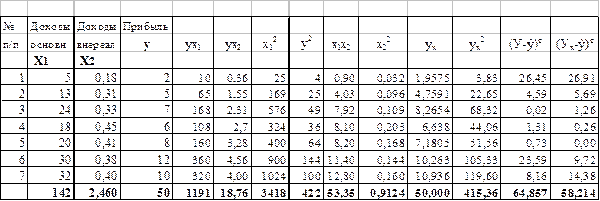
1. Выбор формы уравнения множественной регрессии.
Линейная функция:  a0 + a1x1 + a2x2;
a0 + a1x1 + a2x2;
2. Параметры уравнения множественной регрессии.
Параметры уравнения множественной регрессии рассчитываются методом наименьших квадратов на основе решения системы нормальных уравнений.

 a0n + a1Sx1 + a2Sx2 = Sy, 7a0 +142a1+ 2,46a2 = 50,
a0n + a1Sx1 + a2Sx2 = Sy, 7a0 +142a1+ 2,46a2 = 50,
a0Sx1 + a1Sx21 + a2Sx1x2 = Syx1, 142a0 + 3418a1 + 53,35a2 = 1191,
a0Sx2 + a1Sx1x2 + a2Sx22 = Syx2. 2,46a0 +53,35a1 + 0,9124a2 = 18,76.
а0 = 0,0086; а1 = 0,3148; а2 = 2,1783.  -0,0086+ 0,3148x1 + 2,1783x2
-0,0086+ 0,3148x1 + 2,1783x2
Расчеты показали, что с увеличением доходов от основной деятельности на 1 млрд. руб. прибыль увеличится в среднем на 314,8 млн. руб., а с увеличением внереализационных доходов на 1 млрд. руб. прибыль увеличится в среднем на 2,18 млрд. руб.
3. Расчет множественного коэффициента корреляции
Множественный коэффициент корреляции определяется по формуле:

 = 0,9475
= 0,9475
4. Частные (парные) коэффициенты корреляции
Частные (парные) коэффициенты корреляции определяются по формуле:
 =
=  = 0,94653;
= 0,94653;
 =
=  = 0,67617;
= 0,67617;
 =
=  = 0,68117.
= 0,68117.
5. Строится корреляционная матрица переменных: у, х1, х2.
Корреляционная матрица переменных: у, х1, х2.
| х1 | х2 | у | |
| х1 | 1,0 | 0,68117 | 0,94653 |
| х2 | 0,68117 | 1,0 | 0,67617 |
| у | 0,94653 | 0,67617 | 1,0 |
Наибольшее влияние на прибыль (у) оказывают доходов от основной деятельности (х1).
6. Частные коэффициенты эластичности.
 ;
;  .
.
Расчеты показали, что с увеличением доходов от основной деятельности на 1%. прибыль в среднем увеличивается на 0,894%, а с увеличением доходов от внереализационной деятельности на 1% прибыль увеличивается в среднем на 0,1072 %.
7. Проверка значимости коэффициента множественной корреляции по критерию Фишера-Снедекора.
При Fр > Fкр коэффициент множественной корреляции значимый.


Fкр при  равен 6,94.
равен 6,94.
17,561 > 6,94, значит коэффициент множественной корреляции значимый.
 8. Расчет β-коэффициентов
8. Расчет β-коэффициентов
β-коэффициент определяется по формуле:






 = 0,3148*8,7622/3,0438 = 0,9062;
= 0,3148*8,7622/3,0438 = 0,9062;  = 2,1783*0,0826/3,0438 = 0,0591
= 2,1783*0,0826/3,0438 = 0,0591
b1показывает, что на 0,9062 среднего квадратического отклонения σуизменяется результативный признак упри изменении фактора х1 на величину его среднего квадратического отклонения σх1,и на 0,0591 среднего квадратического отклонения σуизменяется результативный признак упри изменении фактора х2 на величину его среднего квадратического отклонения σх2.Влияние фактора х1 более сильное.
9. Частные коэффициенты детерминации.

 = 0,94653*0,9062 = 0,85775;
= 0,94653*0,9062 = 0,85775;  = 0,67617*0,0591 = 0,03996.
= 0,67617*0,0591 = 0,03996.
Расчеты показали, что на 85,78 % вариация прибыли объясняется вариацией доходов от основной деятельности, на 4,0 % вариацией доходов от внереализационной деятельности, 10,24 % - влияние не учтенных моделью факторов.
10. Множественной коэффициент детерминации.

Таким образом, моделью учтено влияние 89,78 % факторов.
11.  - коэффициенты
- коэффициенты
 - коэффициентыпоказывают влияние каждогоучтенного моделью фактора.
- коэффициентыпоказывают влияние каждогоучтенного моделью фактора.

 ;
;
 .
.
Наибольшее влияние на прибыль оказывает фактор х1 - доходы от основной деятельности.
12. Измерение тесноты связи через корреляционное отношение эмпирических и теоретических значений (у).

 Связь прямая, сильная.
Связь прямая, сильная.
Используется при любой форме связи, прямолинейной и криволинейной.
13. Оценка значимости факторов для включения в модель.
для факторах1:
 ;
;
для факторах2:
.
При Fр > Fкр коэффициент множественной корреляции значимый.
Fкр при  равен 6,94.
равен 6,94.
 - степени свободы;
- степени свободы; 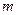 - число параметров уравнения;
- число параметров уравнения;
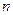 - число наблюдений.
- число наблюдений.
Fкр - Таблица «Значения F- критерия Фишера при уровне значимости 0,05»
Вывод: - для факторах1Fр > Fкр (17,235 > 6,94), коэффициент множественной корреляции значимый.
- для факторах2Fр < Fкр (0,0719 < 6,94), коэффициент множественной корреляции незначимый, можно в модель не включать.
14. Оценка значимости уравнения.

для уравненияFр > Fкр, - уравнение значимо.
Задача 6.4 Определить тесноту связи между прибылью, среднегодовой стоимостью основных производственных фондов и затратами на 100 руб. продукции с помощью коэффициента конкордации.
Исходные данные и расчеты Таблица 5.4
| №№ п/п | Прибыль, млн. руб. | Стоимость ОПФ млн. руб. | Затраты на 100 руб., руб. | Ранжирование факторов | Сумма рангов m | Квадраты сумм рангов m | ||
| Y | X | Z | Ry | Rx | Rz | ∑Ri | (∑Ri)² | |
| 4,1 | ||||||||
| 6,6 | ||||||||
| 3,9 | ||||||||
| 4,2 | ||||||||
| 6,3 | ||||||||
| ∑ |
 Коэффициент конкордации W :
Коэффициент конкордации W :
 | |||
 | |||
 или S = (6-9)²+(14-9)²+(4-9)²+(10-9)²+(11-9)² = 64
или S = (6-9)²+(14-9)²+(4-9)²+(10-9)²+(11-9)² = 64
Связь между приведенными показателями (факторами) сильная, прямая.
Дата добавления: 2014-12-23; просмотров: 325; Мы поможем в написании вашей работы!; Нарушение авторских прав |