Выравнивание по ряду Фурье

Уравнение: ( по одной синусоиде), где

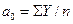5715/12 = 476,25;

2/12 * 182,28 = 30,380; 2/12 * (-82,5) = -13,750

Показатель вариации: 18,52*100/476,25 = 3,89 %

Расчетная таблица Таблица 7.11

месяц	Письменная корреспонд. тыс. ед. У	tф	сos t	sin t	y*сos t	y*sin t
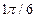		0				0,00	506,63	19,10
			0,866	0,5	399,23	230,50	495,68	1202,99
			0,5	0,866	244,50	423,47	479,53	89,63
						457,00	462,50	30,25
			-0,5	0,866	-225	389,70	449,15	0,72
			-0,866	0,5	-399,23	230,50	443,07	321,63
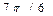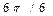
			-1		-459	0,00	445,87	172,40
			-0,866	-0,5	-381,04	-220,00	456,82	282,78
			-0,5	-0,866	-228	-394,90	472,97	287,90
				-1		-472,00	490,0	324,00
			0,5	-0,866	269,50	-466,77	503,35	1271,10
			0,866	-0,5	450,32	-260,00	509,43	111,64
Σ					182,28	-82,50	5715,00	4114,12

Расчет индексов сезонности по фактическим данным, по прямой и по ряду Фурье

Индексы сезонности, % по факту: Индексы сезонности, % по прямой:

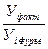
Индексы сезонности, % по Фурье:

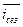
Средний индекс сезонности показывают по фактическим данным колеблемость исследуемого показателя, обусловленную сезонным спросом; по выравненным данным отражает также сезонные колебания.

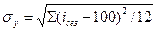
Наилучшее с точки зрения отражения сезонных колебаний нагрузки уравнение выбирают по минимуму среднего квадратического отклонения индексов сезонности от 100 %:

по факту: по прямой:

по Фурье:

Месяцы	У   факт	Индексы сезонности, %	Отклонение от 100 %
по факту	по прямой	по Фурье	по факту	по прямой	по Фурье
		107,30	110,17	100,86	53,24	103,34	0,74
		96,80	98,91	93,00	10,25	1,20	48,96
		102,68	104,41	101,97	7,17	19,43	3,90
		95,96	97,11	98,81	16,34	8,37	1,41
		94,49	95,16	100,19	30,38	23,39	0,04
		96,80	97,03	104,05	10,25	8,83	16,38
		96,38	96,15	102,94	13,12	14,82	8,67
		92,39	91,74	96,32	57,94	68,28	13,55
		95,75	94,63	96,41	18,08	28,86	12,87
		99,11	97,49	96,33	0,80	6,29	13,49
		113,18	110,81	107,08	173,60	116,95	50,17
		109,19	106,41	102,07	84,39	41,15	4,30
Σ		1200,00	1200,01	1200,05	475,55	440,91	174,50

Расчетная таблица Таблица 7.12

Вывод: Расчеты показывают, что ряд Фурье наиболее адекватно отражают колеблемость уровней изучаемого ряда, так как показатели вариации и среднего квадратического отклонения индексов сезонности от 100 % имеют меньшее значение.