
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема 7 Ряды динамики
Цель занятия: Ознакомится с различными видами рядов динамики.
Темпы роста:цепной  , базисный
, базисный  ,
, 
Приросты: цепные 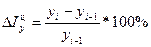 ,
, 
базисные  ,
, 
Абсолютное значение одного процента прироста: 
Среднегодовой темп роста:  или
или  ,
,
Задача 7.1 По данным о доходах за 2004-2009 годы рассчитать темпы роста, прироста базисные и цепные; абсолютный прирост 1 % прироста, среднегодовой рост и прирост доходов за расчётный период.
Исходные данные
Таблица 6.1
| Период | ||||||
| Доходы млн. руб. |
Решение:
Расчетная таблица Таблица 7.2


Среднегодовой рост и прирост доходов за расчётный период определяем, используя формулу средней геометрической: 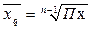


Среднегодовой рост доходов составляет: 106,9 %;
Среднегодовой прирост доходов составляет: 106,9 – 100 = 6,9 %.
Задача 7.2 По данным о ежегодных темпа прироста междугородных телефонных соединений за 2005-2009 вычислить среднегодовой темп роста и прироста за весь период.
Исходные данные Таблица 6.3
| Темпы прироста междугородных телефонных соединений, % | 5,4 | 6,10 | 5,90 | 6,70 | 7,20 |
Решение
Расчетная таблица Таблица 7.4
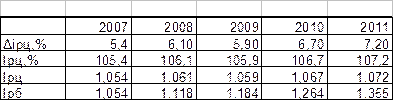
Среднегодовой темп роста:  , прироста:
, прироста: 
 или 106,3%.
или 106,3%.
Среднегодовой темп прироста: 

Задача 7.3 Провести смыкание рядов динамики по данным об объёме продукции за 2003 - 2009 годы по двум периодам: за 2003 - 2005 г.г. и 2005 - 2009 г.г. в относительном и абсолютном выражении.
Исходные данные Таблица 6.5
| Период | |||||||
| Объём продукции, млн. руб. в старых условиях | |||||||
| в новых условиях |
Решение
Расчетная таблица Таблица 6.6
| Период | |||||||
| Объём продукции, млн. руб. в старых условиях | |||||||
| в новых условиях | |||||||
| млн. руб. | 403,8 | 524,1 | |||||
| % | 62,3 | 80,9 | 105,7 | 113,4 | 122,7 | 130,6 |
Год, в котором начинают действовать новые условия и имеются данные, как в старых, так и в новых условиях, называется годом смыкания. В данной задаче – это 2005 год.
Определяем коэффициент смыкания: Ксмык = 648/560 = 1,157
Для определения объёма продукции в новых условиях за 2003 и 2004 годы умножаем их значения в денежных единицах на коэффициент смыкания. Например, за 2003 год объём продукции в новых условиях равен 403,8 ( 349*1,157) млн. руб.
Для определения объёма продукции в новых условиях за весь период в процентах год смыкания принимаем за 100 %.
Объём продукции в новых условиях за 2003 г. будет равен 62,3 (349*100/560) % и т. д.
Объём продукции в новых условиях за 2006 г. будет равен 105,7 (685*100/648) % и т. д.
Задача 7.4 Провести выравнивание нагрузки с использованием 3-х и 5- ти месячных скользящих, рассчитать коэффициенты неравномерности нагрузки.
Исходные данные и расчет скользящих Таблица 6.7
| Месяц | Нагрузка | скользящая 3-х мес | скользящая 5-ти мес | Кнеравн | ||
| тыс. ед. | сумма | средняя | сумма | средняя | % | |
| 107,3 | ||||||
| 96,8 | ||||||
| 102,7 | ||||||
| 95,9 | ||||||
| 94,5 | ||||||
| 96,8 | ||||||
| 96,4 | ||||||
| 92,4 | ||||||
| 95,7 | ||||||
| 99,1 | ||||||
| 113,2 | ||||||
| 109,2 | ||||||
| Всего |
Расчет скользящих проводится в следующей последовательности:
скользящая 3-х мес сумма 511+461+489 = 1461, средняя 1461/3 = 487
сумма 461+489 + 457 = 1407, средняя 1407/3 = 469 и т. д.
скользящая 5-ти мес сумма 511+461+489 + 457 + 450 = 2368, средняя 2368/5 = 474
сумма 461 + 489+457+450 + 461=2318, средняя 2318/5 = 464 и т. д.
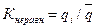
 среднемесячная нагрузка:
среднемесячная нагрузка:  5715/12 = 476,3.
5715/12 = 476,3.
Коэффициенты неравномерности

Рис. 6.1 Выравнивание нагрузки с использованием 3-х и 5- ти месячных скользящих.
Задача 7.5 По данным о доходах за 2005-2010 годы произвести выравнивание динамического ряда и спрогнозировать величину доходов на 2012 год.
Исходные данные Таблица 7.8
| год | Доходы, млн. руб. |
| 549,3 | |
| 764,2 | |
| 1228,4 | |
| 2021,7 | |
| 2975,3 | |
| 3839,8 | |
| 4753,1 |
Решение
Произведем выравнивание динамического ряда по уравнению прямой: y = a0 + a1*t .
Расчетная таблица Таблица 7.9
| год | y | t | t² | Y*t | ỹt | (У-ỹt)2 |
| 549,3 | -3 | -1647,9 | 107,10 | 195540,8 | ||
| 764,2 | -2 | -1528,4 | 839,58 | 5682,14 | ||
| 1228,4 | -1 | -1228,4 | 1572,06 | 118102,2 | ||
| 2021,7 | 2304,54 | 79998,47 | ||||
| 2975,3 | 2975,3 | 3037,02 | 3809,36 | |||
| 3839,8 | 7679,6 | 3769,50 | 4942,09 | |||
| 4753,1 | 14259,3 | 4501,98 | 63061,25 | |||
| ∑ | 16131,8 | 20509,5 | 16131,78 | 471136,3 |
Уравнение прямой: y = a0 + a1*t. a0 = ∑y/n = 16131,8/7 = 2304,54;
a1 = ∑yt/∑t² = 20509,5/28 = 732,48. ỹt = 2304,54 + 732,48*t
 = 259,43;
= 259,43;  = 259,43*100/2304,54 = 11,26 %.
= 259,43*100/2304,54 = 11,26 %.
Уравнение регрессии можно использовать в целях прогнозирования, т.к. v ‹ 33%
ỹ(2012) = 2304,54+732,48*4 = 5234,46 млн. руб.
Величина доверительного интервала.


где: α – коэффициент доверия (обычно выбирается 0,05);
tα – находится по таблице «t- критерия Стьюдента» (зависит от α и числа степеней свободы v = n – m =7-2=5). tα = 2,5706
n - число уровней ряда (в примере n =7);
m - число параметров уравнения (для уравнения прямой m=2).
SYt - среднее квадратическое отклонение от тренда.
 |  | ||
ỹ(2012) = 5234,46 ± 298,24 Доверительный интервал: min 4936,21 max 5532,69 млн. руб.
Величина относительной ошибки: S*100/ŷt %. 306,96*100/2304,54 = 13,32%.
Задача 7.6. Провести выравнивание нагрузки предприятия связи по прямой и по ряду Фурье. Определить функцию, наиболее адекватно отражающую колеблемость уровней изучаемого ряда.
Дата добавления: 2014-12-23; просмотров: 265; Мы поможем в написании вашей работы!; Нарушение авторских прав |