Групування з використанням нерівних інтервалів

Групування на нерівні інтервали застосовуються для опису статистичних даних, що мають явну асиметрію розподілу частот і частостей. Ширину і межі цих інтервалів встановлюють на основі логічного аналізу попередніх зведень про якісні і кількісні характеристики досліджуваного явища.

В економіці широко застосовуються групування економічних об’єктів з поділом їх на великі, дрібні та середні. Однак такий розподіл залежить від галузевих особливостей і неминуче пов’язаний з низкою умовностей. Наприклад, хлібозавод з чисельністю працівників більш 300 чоловік вважається великим, в той час, як машинобудівний завод з такою ж чисельністю працівників може бути віднесений до групи дрібних або середніх підприємств.

В практичній роботі в якості одного з можливих рішень задачі групування підприємств по розміру валового доходу рекомендується використовувати досить просту формалізовану процедуру розподілу підприємств на групи.

Процедура виділення груп об’єктів з нерівними інтервалами досліджуваної ознаки наступна. Необхідно проранжувати значення ознаки. Потім весь інтервал його можливих значень слід розділити на два інтервали, що відокремлені друг від друга середнім значенням показника .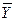

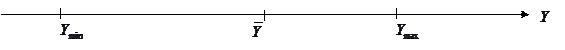На першому інтервалі будуть розташовані значення досліджуваної ознаки менше середнього значення 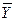. На другому інтервалі будуть розташовані значення досліджуваної ознаки більше, ніж середнє значення .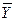

У випадку асиметричного розподілу точка, що відповідає середньому значенню ознаки 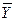, не буде поділяти інтервал на рівні частини, а буде зміщена до якого-небудь з кінців інтервалу.

Вибираємо з двох інтервалів, розділених значенням середньої величини 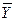, інтервал найменшої довжини, для чого порівнюємо по модулю величини 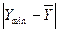і . Довжину найменшого з двох порівнюваних інтервалів поділяємо навпіл і отримане значення додаємо до середнього 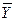і віднімаємо від нього. Одержуємо координати двох точок 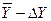і 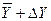, які відзначаємо на числовій осі варіаційного ряду вліво і вправо від середнього значення .

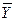В результаті числова вісь, що відповідає проранжованому варіаційному ряду досліджуваної ознаки, розділяється на три інтервали , та , довжини яких можуть бути інтерпретовані як величини що відмежовують дрібні, середні і великі одиниці сукупності.

При досить великій величині розмаху варіації досліджуваної ознаки процедура дроблення всієї числової осі може бути повторена, у результаті чого будуть визначені границі груп самих дрібних, середніх, більше середнього і самих великих об’єктів.

Після встановлення границь інтервалів варто розробити таблицю частот і частостей, побудувати гістограму розподілу підприємств.

Результати групувань з використанням рівних і нерівних інтервалів варто проаналізувати і зробити попередній висновок щодо закономірності розподілу підприємств за розміром досліджуваного показника. Крім того, необхідно вказати спосіб групування, що дав більш чітке представлення щодо закономірностей розподілу розподілу досліджуваного показника.