Парний кореляційно-регресійний аналіз залежностей

5.1 Кореляційний аналіз парних зв'язків

Кореляційний аналіз проводять з метою оцінки сили й істотності залежності результативної перемінної від факторних перемінних. Якщо факторних перемінних небагато (у загальному випадку ), то на першому етапі дослідження проводять аналіз залежності результативної перемінної від кожної факторної перемінної

.

Таким чином, у практичній роботі необхідно провести кореляційний аналіз залежності валового доходу підприємства від середньорічної вартості основних фондів від средньоспискової чисельності працюючих 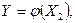, від фондовіддачі , від фондоозброєності і від продуктивності праці .

Для виявлення наявності залежності однієї перемінної від іншої необхідно побудувати кореляційне поле і розрахувати коефіцієнт парної кореляції. Рекомендації з виконання цієї частини роботи наводяться в літературі по дисципліні [1-3, 7-12]. Оскільки в літературі для розрахунку коефіцієнта парної кореляції приводяться різні формули, то в курсовій роботі рекомендується використовувати наступну

,

де ; ;

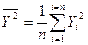Розрахунок середніх для добутків і середніх для квадратів значень досліджуваних перемінних приводиться в таблицях 6 і 7.

Результати кореляційного аналізу представляються в пояснювальній записці. Для кожної пари зв’язків в записці потрібно привести графік кореляційного поля, розрахунок коефіцієнта парної кореляції і висновки щодо істотності зв’язку перемінних.

5.2 Регресійний аналіз парних зв'язків

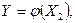
Методика регресійного аналізу викладена в літературі [1-3, 7-12]. В практичній роботі потрібно представити найбільш важливі результати регресійного аналізу. Зокрема для кожної пари зв’язків повинні бути дані відповіді на наступні запитання:

1) яка форма зв’язку (пряма або зворотня, лінійна або нелінійна) має місце між і кожною з досліджуваних факторних перемінних ;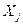

2) яке рівняння регресії найкраще описує залежність між та ;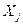

3) чи є це рівняння статистично значимим.

Для вибору форми зв’язку потрібно використовувати раніше побудований графік із зображенням кореляційного поля; побудувати емпіричну лінію регресії; по її вигляду визначити, чи є залежність прямою або зворотньою; яке рівняння парної регресії доцільно використовувати для апроксимації емпіричної лінії регресії.

Визначення форми зв’язку. Якщо зі збільшенням значень перемінної 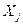, значення перемінної також збільшуються, то має місце пряма лінійна (рис. 1а) або пряма нелінійна (рис. 16) залежність. Якщо зі збільшенням значень перемінної 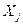, значення перемінної зменшуються, то має місце зворотній лінійний (рис.2а), або нелінійний (рис.2б) зв’язок.

При виконанні дослідження варто враховувати, що у всіх випадках, коли має місце нелінійний зв’язок, а сила зв’язку неправомірно намагаються оцінити за допомогою коефіцієнта кореляції, його значення отримуються незначними, а іноді близькими до нуля.

Якщо кореляційне поле „розмите” і не дозволяє виявити закономірності між зміною значень перемінних 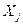і , то є підстави вважати, що зв’язок між ними відсутній (рис.3).

При виявленні форми зв’язку між перемінними важливо переконатися в тому, що спостереження мають приблизно однакову варіацію щодо передбачуваної теоретичної лінії регресії. У випадку, коли дані розподіляються вздовж лінії регресії нерівномірно (рис.4), вважається що метод найменших квадратів непридатний для підбора лінії регресії.

Вибір рівняння регресії. У випадку, коли між перемінними і 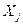передбачається прямий або лінійний зв’язок, обирають рівняння вигляду

,

де - теоретичне значення результативної перемінної, розраховане за рівнянням регресії за умови, що об’єкт з номером має значення факторної перемінної, яке дорівнює ;

Таблиця 6 – Розрахунок середньої суми квадратів значень перемінних та суми добутків

... ...
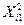
Сума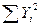
Середнє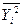

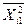
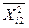
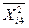
Таблиця 7 – Розрахунок середньої суми квадратів добутків факторних перемінних

	Для	Для	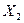Для	Для
... ...
Сума
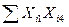
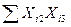
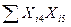
Середнє

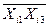
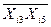
а б

Рис.1 - Пряма лінійна (а) і пряма нелінійна (б) кореляційна залежність

а б

Рис.2 - Зворотня лінійна (а) і зворотня нелінійна (б) кореляційна залежність

Рис.3 – Відсутність кореляційного зв’язку між перемінними

Рис.4 – Регресія з нерівномірною варіацією, яка призводить до викривлення оцінок

- параметри рівняння;

- значення 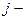ї факторної перемінної на -му спостережені;

- випадкова похибка результативної перемінної.

Далі розраховують невідомі значення параметрів і за даними вибірки.

або

У випадку, коли між перемінними передбачається пряма або зворотня нелінійна залежність, рівняння регресії рекомендується підібрати по Додатку Д. Далі використовуючи прийом лінеаризації вихідних значень перемінних і параметрів (Додаток Д), варто перевести обране рівняння до лінійного виду і по відомих формулах обчислити значення параметрів

і .

Слід враховувати, що іноді тенденція в розкиді точок в поле кореляції може бути не видна через недолік обраного масштабу зображення. В зв’язку з цим рекомендується використовувати техніку побудови багаторівневих графіків. Вона припускає, крім основного графика, побудову декількох додаткових графіків, які являють собою вертикально і горизонтально стиснуті зображення основного графіка. Цей стиск графіків полегшує ідентифікацію затіненої (що чітко не виявляється) тенденції розкиду точок поля кореляції двох перемінних.

Приклад. Вивчається залежність валового доходу підприємства ( ) від середньорічної вартості основних виробничих фондів , середньорічної чисельності працюючих ; фондовіддачі ; фондоозброєності та продуктивності праці . Для перевірки гіпотези отримані вибірковим методом (з Додатка А) дані по 19 підприємствам (табл.8).

Потрібно побудувати кореляційні поля і вибрати рівняння регресії для опису залежностей між досліджуваними показниками.

Таблиця 8 – Вихідні дані до прикладу

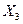
				0,93074	2,35746	2,53289
				0,98625	2,42647	2,46029
				1,23265	3,09215	2,50853
				5,59899	3,67285	2,29698
				1,50822	3,99171	2,64663
				1,50570	4,21992	2,80263
				1,52354	4,14974	2,72375
				1,51798	4,14610	2,73132
				1,48056	4,10172	2,77038
				1,69878	4,23283	2,49168
				1,53059	4,36510	2,85191
				1,52323	4,53440	2,07683
				1,56168	4,54261	2,90879
				1,59141	4,30142	2,70290
				1,52638	4,33953	2,84302
				1,52750	5,41386	3,54427
				1,46464	4,37927	2,99001
				1,52962	4,41358	2,83541
				1,24738	4,76131	3,81706
Всього				27,48585	77,44204	53,48530

На рис.5, 6, 7, 8 і 9 представлені багаторівневі графіки кореляційних полів, результати апроксимації тенденцій у розкиді точок лінійними і нелінійними формами зв’язку. Ці рисунки добре ілюструють вплив масштабу зображення полів кореляції на результати вибору форми зв’язку двох перемінних.

Якщо для опису регресії можуть бути використані кілька рівнянь, то кращим з них звичайно вважається те, що має найбільше значення критерію Фішера (однак можна використовувати й інші критерії, наприклад, найбільше значення коефіцієнта кореляції, найменшу відносну помилку прогнозування тощо).

Критерій Фішера використовується для перевірки різних гіпотез. У випадку перевірки гіпотези про значущість обраної моделі регресії спочатку розраховують його емпіричне значення.

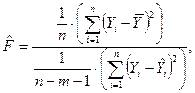
де - кількість факторних ознак моделі (для моделі парної регресії ).

Це значення порівнюють із критичним значенням, що знаходять по таблицях (Додаток Е) для обраного рівня довірчої імовірності (прийняти рівним 0,95) на перетинанні стовпця, що відповідає числу ступенів волі 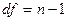, і рядка, що відповідає числу ступенів волі .

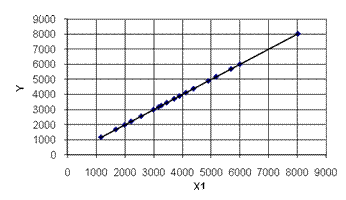
а

б

Рис.5 – Поля кореляції для перемінної та лінії регресії, які їх апроксимують: а) лінійний варіант; б) нелінійний варіант (логарифмічна крива)

а

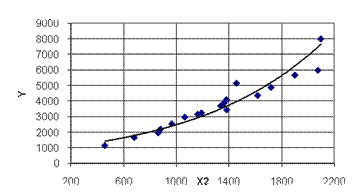
б

Рис.6 - Поля кореляції для перемінної та лінії регресії, які їх апроксимують: а) лінійний варіант; б) нелінійний варіант (експонента)

а

б

Рис.7 - Поля кореляції для перемінної 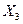та лінії регресії, які їх апроксимують: а) лінійний варіант; б) нелінійний варіант (полінома)

а

б

Рис.8 - Поля кореляції для перемінної та лінії регресії, які їх апроксимують: а) лінійний варіант; б) нелінійний варіант (логарифмічна крива)

а

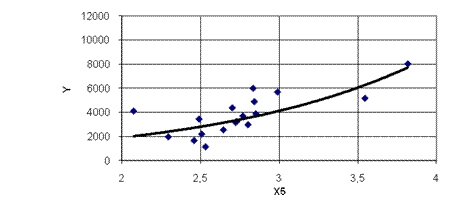
б

Рис.9 - Поля кореляції для перемінної та лінії регресії, які їх апроксимують: а) лінійний варіант; б) нелінійний варіант (експонента)

Якщо розрахункове значення більше критичного, то модель вважається значущою на обраному рівні довірчої імовірності. В противному випадку модель вважається незначущою. Однак при зниженні рівня довірчої імовірності вона може виявитися статистично значущою.

Розрахунок для обраних форм зв’язку перемінних варто виконати в таблицях, а хід перевірки гіпотез і зроблені висновки описати в пояснювальній записці.