Добір факторів для багатофакторної моделі

Модель множинної регресії повинна включати, фактори, які мають сильний зв’язок з результативною перемінною і не мають сильного зв’язку між собою. Взаємозв’язок факторних перемінних прийнято називати мультиколінеарністю. Мультиколінеарність розглядається як небажане явище.

Добір факторів, що підлягають включенню в модель регресії, рекомендується виконати за спрощеною методикою, не прибігаючи до методів багатокрокового кореляційно-регресійного аналізу.

Для добору факторів, що підлягають включенню в модель регресії, рекомендується розрахувати всі елементи матриці парних коефіцієнтів кореляції (табл.9).

Матриця парних коефіцієнтів кореляції є симетричною: значення коефіцієнтів кореляції над головною діагоналлю і під нею рівні (тобто тощо). Значення елементів, розташованих на головній діагоналі матриці завжди дорівнюють одиниці.

Розташування перемінних у цій матриці може бути й іншим.

Таблиця 9 – Загальний вигляд матриці парних коефіцієнтів кореляції

Перемінні
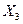
	1,0
		1,0
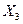
			1,0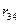
				1,0
					1,0
						1,0

Заповнення матриці значеннями парних коефіцієнтів кореляції роблять у такий спосіб. Коефіцієнти парної кореляції між результативної перемінною і факторними перемінними обчислені раніше (п.3.1), тому їхні значення записують в останній стовпець і останній рядок матриці. Далі, починаючи з першого рядка, роблять розрахунок відсутніх у матриці коефіцієнтів парної кореляції. Для розрахунку використовується формула вже відома з курсу „Статистика” коефіцієнта парної кореляції між перемінними з порядковими номерами і .

Для розрахунку використовуються суми і середні, обчислені в табл.7 і табл.8. Матрицю парних коефіцієнтів кореляції потрібно проаналізувати і виділити пари факторних перемінних, які мають між собою високий кореляційний зв’язок ( ). У кожній з таких пар виключити з подальшого розгляду ту факторну перемінну, яка має менший коефіцієнт кореляції з результативною перемінною. Для подальшого аналізу доцільно залишити дві-три факторні перемінні.

Приклад. Вивчається залежність валового доходу підприємства ( ) від середньорічної вартості основних виробничих фондів , середньорічної чисельності працюючих ; фондовіддачі ; фондоозброєності та продуктивності праці . На підставі раніше приведених вихідних даних (табл.8) розраховані коефіцієнти парної кореляції між усіма перемінними в припущенні, що усі вони мають лінійну форму зв’язку.

Результати розрахунків коефіцієнтів приведені в табл.10.

Таблиця 10 – Вихідна матриця парних коефіцієнтів кореляції (приклад)

Перемінні
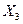
	1,00000
	0,97185	1,00000
	0,98190	0,95827	1,00000
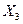
	0,49370	0,30479	0,46313	1,00000
	0,76283	0,84296	0,67057	0,05252	1,00000
	0,85150	0,76241	0,76382	0,74584	0,69968	1,00000

Аналіз матриці показує, що між факторними перемінними і існує сильний внутрішній кореляційний зв’язок (коефіцієнт кореляції дорівнює 0,95827). З них трохи сильніше впливає на результативний показник факторна перемінна (коефіцієнт кореляції 0,9819). Тому виключаємо з подальшого розгляду факторну перемінну .

Матриця парних коефіцієнтів кореляції для змінних, що залишилися, має такий вигляд (табл.11).

Таблиця 11 – Зменшена матриця парних коефіцієнтів кореляції (приклад)

Перемінні
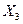
	1,00000
	0,98190	1,00000
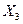
	0,49370	0,46313	1,00000
	0,76283	0,67057	0,05252	1,00000
	0,85150	0,76382	0,74584	0,69968	1,00000

У цій матриці немає факторних перемінних, між якими є тісний кореляційний зв’язок з коефіцієнтом кореляції більш 0,8.

Таким чином, для подальшого дослідження впливу на річний валовий доход підприємства слід залишити чотири факторні перемінні - средньоспискову чисельність працюючих , фондовіддачу , фондоозброєність і продуктивність праці .