
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Оцінка параметрів багатофакторної лінійної моделі регресії
При вирішенні задачі як від руки, так і на ЕОМ, параметри лінійної багатофакторної моделі варто розрахувати за методом найменших квадратів (МНК) з використанням матриць.
Оцінка параметрів багатофакторної лінійної моделі регресії методом МНК із використанням матриць. У матричному вигляді лінійна моделі регресії записується в такий спосіб
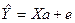 ,
,
де  - вектор теоретичних значень залежної перемінної,
- вектор теоретичних значень залежної перемінної,  ;
;
 - матриця значень незалежних перемінних розміром
- матриця значень незалежних перемінних розміром  ;
;
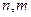 - кількість спостережень та кількість невідомих параметрів;
- кількість спостережень та кількість невідомих параметрів;
 - вектор оцінок параметрів моделі,
- вектор оцінок параметрів моделі,  ;
;
 - вектор випадкових помилок, які не залежать від моделі.
- вектор випадкових помилок, які не залежать від моделі.
Оцінку параметрів цієї моделі виконують методом найменших квадратів. Він дозволяє вибрати параметри моделі таким чином, щоб сума квадратів відхилень значень результативної перемінної  , що спостерігаються, від значень, обчислених по моделі
, що спостерігаються, від значень, обчислених по моделі  , була мінімальною
, була мінімальною
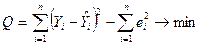
або в матричному вигляді

Якщо продиференцювати  по
по  , прирівняти похідну до нуля та зробити інші перетворення, то буде отримано вираз для визначення параметрів моделі
, прирівняти похідну до нуля та зробити інші перетворення, то буде отримано вираз для визначення параметрів моделі

Стосовно до лінійної моделі регресії матриці, що використовуються для оцінки невідомих параметрів, мають наступний вигляд


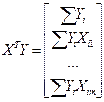
Підсумовування виробляється за кількістю спостережень  .
.
Після визначення значень параметрів, слід записати числову моделі регресії і дати їм економічну характеристику.
Приклад. На підставі попереднього парного кореляційно-регресійного аналізу встановлена залежність залежність валового доходу підприємства (  ) від чотирьох показників: середньорічної середньорічної чисельності працюючих
) від чотирьох показників: середньорічної середньорічної чисельності працюючих  ; фондовіддачі
; фондовіддачі  ; фондоозброєності
; фондоозброєності  та продуктивності праці
та продуктивності праці  . Усі факторні перемінні не мають мультиколінеарних зв’язків. Передбачається, що багатофакторна модель регресії повинна бути лінійною
. Усі факторні перемінні не мають мультиколінеарних зв’язків. Передбачається, що багатофакторна модель регресії повинна бути лінійною

Потрібно оцінити параметри цієї моделі методом найменших квадратів.
Для оцінки параметрів використовуємо дані, що раніше розглядалися по 19 підприємствам без фактора  . Вихідні дані для оцінки параметрів моделі регресії приведено в табл.12, доповненої фіктивною перемінною
. Вихідні дані для оцінки параметрів моделі регресії приведено в табл.12, доповненої фіктивною перемінною 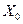 .
.
Таблиця 12 - Вихідні дані до приклада оцінки параметрів моделі регресії

| 
| 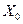
| 
| 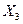
| 
| 
|
| 0,93074 | 2,53289 | 2,35746 | ||||
| 0,98625 | 2,46029 | 2,42647 | ||||
| 1,23265 | 2,50853 | 3,09215 | ||||
| 5,59899 | 2,29698 | 3,67285 | ||||
| 1,50822 | 2,64663 | 3,99171 | ||||
| 1,50570 | 2,80263 | 4,21992 | ||||
| 1,52354 | 2,72375 | 4,14974 | ||||
| 1,51798 | 2,73132 | 4,14610 | ||||
| 1,48056 | 2,77038 | 4,10172 | ||||
| 1,69878 | 2,49168 | 4,23283 | ||||
| 1,53059 | 2,85191 | 4,36510 | ||||
| 1,52323 | 2,07683 | 4,53440 | ||||
| 1,56168 | 2,90879 | 4,54261 | ||||
| 1,59141 | 2,70290 | 4,30142 | ||||
| 1,52638 | 2,84302 | 4,33953 | ||||
| 1,52750 | 3,54427 | 5,41386 | ||||
| 1,46464 | 2,99001 | 4,37927 | ||||
| 1,52962 | 2,83541 | 4,41358 | ||||
| 1,24738 | 3,81706 | 4,76131 |
Оцінимо параметри  цієї моделі за методом найменших квадратів з використанням техніки матричного рахування [4].
цієї моделі за методом найменших квадратів з використанням техніки матричного рахування [4].
Сформуємо матриці необхідні для оцінки параметрів.


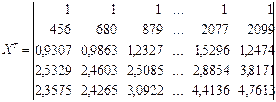


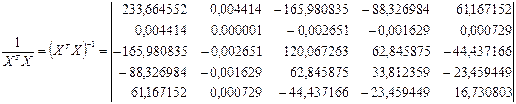
Знайдемо вектор параметрів моделі регресії
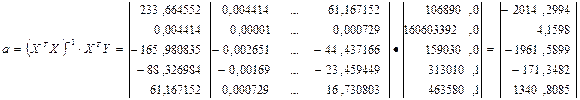
Записуємо модель регресії з використанням числових значень параметрів регресії

та визначаємо область змінення факторних перемінних


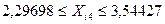
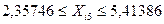
Дата добавления: 2014-12-23; просмотров: 1062; Мы поможем в написании вашей работы!; Нарушение авторских прав |