Теоретична довідка. При проведенні різних вибіркових досліджень (маркетингових, клінічних, епідеміологічних, соціологічних) дуже часто виникає необхідність оцінити узгодженість

При проведенні різних вибіркових досліджень (маркетингових, клінічних, епідеміологічних, соціологічних) дуже часто виникає необхідність оцінити узгодженість думок експертів. Це надалі дозволяє виявити різні підходи експертів до оцінки різних явищ (ознак, критеріїв), що дозволяє потім провести поглиблений аналіз ситуації і прийняти обґрунтоване рішення.

У зв'язку з природою даних, які є результатами експертних оцінок (зазвичай бали), для їх аналізу зазвичай використовуються рангові (непараметричні) методи.

Для того, щоб оцінити узгодженість думок двох експертів при їх оцінці ряду ознак (або об'єктів, що має значення при рішенні завдання ранжирування), можна скористатися коефіцієнтом кореляції Спірмена або коефіцієнтом кореляції Кендалла.

В разі, якщо експертів не два, а більш (наприклад, при з'ясуванні узгодженості думок групи експертів), використовується коефіцієнт конкордації, запропонований Кендаллом:

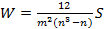(4.1)

де S= , n - кількість аналізованих об'єктів, m - кількість експертів, Rij - ранг j-го об'єкту, який привласнений йому i-им експертом.

Слід звернути увагу на відмінність значень коефіцієнта конкордації від коефіцієнта кореляції, оскільки він існує в межах від 0 до 1. Якщо думки експертів повністю протилежні, коефіцієнт конкордации дорівнює нулю (W = 0), а коефіцієнт кореляції в цьому випадку буде рівний -1.

За наявності в'язок (однакових значень) формула (4.1) набуває наступного вигляду:

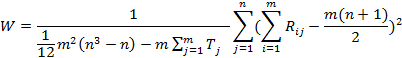
(4.2)

де 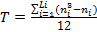, при цьому L_i - число зв'язок, n_i - кількість елементів в i-й в'язці для j-го експерта.