Виды и формы средних величин

Категорию средней можно раскрыть через понятие ее определяющего свойства,согласно которомусредняя, являясь обобщающей характеристикой всей совокупности, должна ориентироваться на определенную величину, связанную со всеми единицами этой совокупности. Эту величину можно представить в виде функции:

f (х₁, х₂, ..., х_n)

Если в приведенной выше функции все величины х₁, х₂, ..., х_n заменить их средней величиной , то значение этой функции должно остаться прежним:

Исходя из данного равенства и определяется средняя.

На практике определить среднюю во многих случаях можно через исходное соотношение средней (ИСС) или ее логическую формулу:

Так, например, для расчета средней заработной платы работников предприятия необходимо общий фонд заработной платы разделить на число работников:

Числитель исходного соотношения средней представляет собой определяющий показатель.

От того, в каком виде представлены исходные данные для расчета средней, зависит, каким именно образом будет реализовано ее исходное соотношение. В каждом конкретном случае для реализации исходного соотношения потребуется один из следующих видов средней величины:

· средняя арифметическая;

· средняя гармоническая;

· средняя геометрическая;

· средняя квадратическая, кубическая и т.д.

Перечисленные средние объединяются в общей формуле средней степенной (при различной величине k):

Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными.

Простая степенная средняя считается по не сгруппированным данным и имеет следующий общий вид:

где – значение (варианта) осредняемого признака; k– показатель степени средней; n – число значений признака.

Взвешенная степенная средняясчитается по сгруппированным данным и имеет общий вид

где – значение (варианта) осредняемого признака или серединное значение интервала, в котором измеряется варианта;

k– показатель степени средней;

f_i – частота, показывающая, сколько раз встречается i-e значение осредняемого признака.

Изменение показателя степени k приводит в каждом отдельном случае к определенному виду средней:

Показатель степени	Вид средней	Формулы средней
Простая	Взвешенная
k = -1	Средняя гармоническая
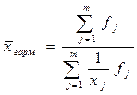
k = 0	Средняя геометрическая
k = 1	Средняя арифметическая
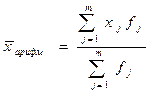
k = 2	Средняя квадратическая

Если рассчитать все виды средних для одних и тех же исходных данных, то значения их окажутся неодинаковыми. Здесь действует правило мажорантности средних: с увеличением показателя степени k увеличивается и соответствующая средняя величина:

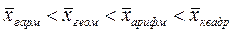
Выбор вида степенной средней определяется экономическим содержанием задачи и наличием данных.