Линейного преобразования

Определение: Пусть L – заданное n- мерное линейное пространство. Ненулевой вектор L называется собственным вектором линейного преобразования А, если существует такое число l, что выполняется равенство:

A .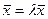

При этом число l называется собственным значением (характеристическим числом) линейного преобразования А, соответствующего вектору .

Определение: Если линейное преобразование А в некотором базисе , ,…, имеет матрицу А = , то собственные значения линейного преобразования А можно найти как корни l₁, l₂, … ,l_n уравнения:

Это уравнение называется характеристическим уравнением, а его левая часть- характеристическим многочленом линейного преобразования А.

Пример. Найти характеристические числа и собственные векторы линейного преобразования с матрицей А = .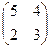

Запишем линейное преобразование в виде:

Составим характеристическое уравнение:

l² - 8l + 7 = 0;

Корни характеристического уравнения: l₁ = 7; l₂ = 1;

Для корня l₁ = 7: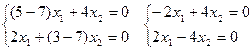

Из системы получается зависимость: x₁ – 2x₂ = 0. Собственные векторы для первого корня характеристического уравнения имеют координаты: (t; 0,5t) где t- параметр.

Для корня l₂ = 1:

Из системы получается зависимость: x₁ + x₂ = 0. Собственные векторы для второго корня характеристического уравнения имеют координаты: (t; -t) где t- параметр.

Полученные собственные векторы можно записать в виде:

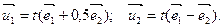
Пример. Найти характеристические числа и собственные векторы линейного преобразования А, матрица линейного преобразования А = .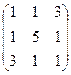

Составим характеристическое уравнение:

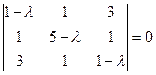
(1 - l)((5 - l)(1 - l) - 1) - (1 - l - 3) + 3(1 - 15 + 3l) = 0

(1 - l)(5 - 5l - l + l² - 1) + 2 + l - 42 + 9l = 0

(1 - l)(4 - 6l + l²) + 10l - 40 = 0

4 - 6l + l² - 4l + 6l² - l³ + 10l - 40 = 0

-l³ + 7l² – 36 = 0

-l³ + 9l² - 2l² – 36 = 0

-l²(l + 2) + 9(l² – 4) = 0

(l + 2)(-l² + 9l - 18) = 0

Собственные значения: l₁ = -2; l₂ = 3; l₃ = 6;

1) Для l₁ = -2:

Если принять х₁ = 1, то Þ х₂ = 0; x₃ = -1;

Собственные векторы:

2) Для l₂ = 3: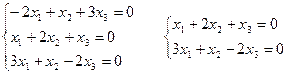

Если принять х₁ = 1, то Þ х₂ = -1; x₃ = 1;

Собственные векторы:

3) Для l₃ = 6:

Если принять х₁ = 1, то 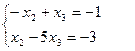Þ х₂ = 2; x₃ = 1;

Собственные векторы: