Определение. Числа и называются комплексно – сопряженными.

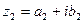Определение. Два комплексных числа и называются равными, если соответственно равны их действительные и мнимые части:

Определение. Комплексное число равно нулю, если соответственно равны нулю действительная и мнимая части.

Понятие комплексного числа имеет геометрическое истолкование. Множество комплексных чисел является расширением множества действительных чисел за счет включения множества мнимых чисел. Комплексные числа включают в себя все множества чисел, которые изучались ранее. Так натуральные, целые, рациональные, иррациональные, действительные числа являются, вообще говоря, частными случаями комплексных чисел.

Если любое действительное число может быть геометрически представлено в виде точки на числовой прямой, то комплексное число представляется точкой на плоскости, координатами которой будут соответственно действительная и мнимая части комплексного числа. При этом горизонтальная ось будет являться действительной числовой осью, а вертикальная - мнимой осью.

у

A(a, b)

r b

j

0 a x

Таким образом, на оси ОХ располагаются действительные числа, а на оси ОY – чисто мнимые.

С помощью подобного геометрического представления можно представлять числа в так называемой тригонометрической форме.