
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Действия с комплексными числами
Основные действия с комплексными числами вытекают из действий с многочленами.
1) Сложение и вычитание

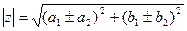
2) Умножение
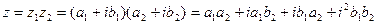

В тригонометрической форме:
 ,
, 

В случае комплексно – сопряженных чисел:

3) Деление



В тригонометрической форме:

4) Возведение в степень
Из операции умножения комплексных чисел следует, что

В общем случае получим:
 ,
,
где n – целое положительное число.
Это выражение называется формулой Муавра.
(Абрахам де Муавр (1667 – 1754) – английский математик)
Формулу Муавра можно использовать для нахождения тригонометрических функций двойного, тройного и т.д. углов.
Пример. Найти формулы sin2j и cos2j.
Рассмотрим некоторое комплексное число 
Тогда с одной стороны  .
.
По формуле Муавра: 
Приравнивая, получим 
Т.к. два комплексных числа равны, если равны их действительные и мнимые части, то


Получили известные формулы двойного угла.
5) Извлечение корня из комплексного числа

Возводя в степень, получим:

Отсюда: 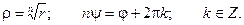

Таким образом, корень n – ой степени из комплексного числа имеет n различных значений.
Пример. Даны два комплексных числа  . Требуется а) найти значение выражения
. Требуется а) найти значение выражения  в алгебраической форме, б) для числа
в алгебраической форме, б) для числа 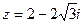 найти тригонометрическую форму, найти z20, найти корни уравнения
найти тригонометрическую форму, найти z20, найти корни уравнения 
a) Очевидно, справедливо следующее преобразование:

Далее производим деление двух комплексных чисел:

Получаем значение заданного выражения: 16(-i)4 = 16i4 =16.
б) Число 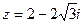 представим в виде
представим в виде 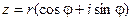 , где
, где
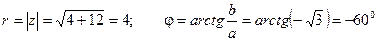
Тогда  .
.
Для нахождения  воспльзуемся формулой Муавра.
воспльзуемся формулой Муавра.


Если  , то
, то 
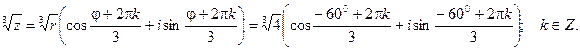
Дата добавления: 2014-12-30; просмотров: 309; Мы поможем в написании вашей работы!; Нарушение авторских прав |