Предел функции при стремлении аргумента к бесконечности

Определение. Число А называется пределом функции f(x) при х®¥, если для любого числа e>0 существует такое число М>0, что для всех х, ïхï>M выполняется неравенство

При этом предполагается, что функция f(x) определена в окрестности бесконечности.

Записывают:

Графически можно представить:

y y

A A

0 х 0 x

y y

A A

0 0 x x

Аналогично можно определить пределы для любого х>M и

для любого х<M.

Основные теоремы о пределах

Теорема 1. , где С = const.

Следующие теоремы справедливы при предположении, что функции f(x) и g(x) имеют конечные пределы при х®а.

Теорема 2.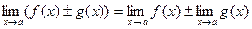

Доказательство этой теоремы будет приведено ниже.

Теорема 3.

Следствие.

Теорема 4. при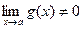

Теорема 5. Если f(x)>0 вблизи точки х = а и , то А>0.

Аналогично определяется знак предела при f(x) < 0, f(x) ³ 0, f(x) £ 0.

Теорема 6. Если g(x) £ f(x) £ u(x) вблизи точки х = а и , то и .

Пример. Найти предел

Так как tg5x ~ 5x и sin7x ~ 7x при х ® 0, то, заменив функции эквивалентными бесконечно малыми, получим:

Пример. Найти предел .

Так как 1–cosx = 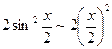при х®0, то .

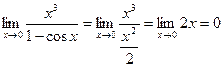Пример. Найти предел

Если a и b - бесконечно малые при х®а, причем b - бесконечно малая более высокого порядка, чем a, то g = a + b - бесконечно малая, эквивалентная a. Это можно доказать следующим равенством .

Тогда говорят, что a - главная частьбесконечно малой функции g.

Пример. Функция х² +х – бесконечно малая при х®0, х – главная часть этой функции. Чтобы показать это, запишем a = х², b = х, тогда

.