
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Контрольная работа №1 3 страница
Задание 8.
Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей А.
А = 
Задание 9.
Найти пределы функции, не пользуясь правилом Лопиталя.
а) 
| в) 
|
б) 
| г) 
|
Задание 10.
Дано комплексное число z = -6 / (1- i  ). Требуется 1) записать число z в алгебраической и тригонометрической формах; 2) найти все корни уравнения w3+z =0.
). Требуется 1) записать число z в алгебраической и тригонометрической формах; 2) найти все корни уравнения w3+z =0.
Вариант 15
Задание 1.
Дана система линейных уравнений

Доказать её совместность и решить двумя способами: 1) Методом Гаусса; 2) средствами матричного исчисления.
Задание 2.
Даны векторы a (1; 2; 1), b (2; -1; 3), c (3; -1; 4), d (5; 1; 6) в некотором базисе. Показать, что векторы а, в, с образуют базис, и найти координаты вектора dв этом базисе.
Задание 3.
Даны координаты вершины пирамиды А1А2А3А4:A1 (2; 4; 3), A2 (4; 6; 6), A3 (4; 2; 0), A4 (1; 2; 6).
Найти:1)длину ребра А1А2; 2)угол между ребрами А1А2 И А1А4; 3)угол между ребром А1А4 и гранью А1А2А3; 4)площадь грани А1А2А3; 5)объем пирамиды; 6)уравнение прямой А1А2; 7)уравнение плоскости А1А2А3; 8)уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертеж.
Задание 4.
Дана вершина треугольника А (3; 9) и уравнения медиан: y – 6 = 0; 3x – 4y + 9 = 0. Найти координаты двух вершин. Сделать чертеж.
Задание 5.
Написать уравнение множества точек, одинаково удаленных от точки F (0; 2) и прямой y = 4. Найти точки пересечения этой кривой с осями координат и построить ее.
Задание 6.
Линия задана уравнением в полярной системе координат 
Требуется:1)построить линию по точкам, начиная от 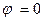 до
до  и придавая
и придавая 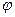 значения через промежуток
значения через промежуток 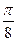 ; 2)найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3)по уравнению в декартовой прямоугольной системе координат определить, какая это линия.
; 2)найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3)по уравнению в декартовой прямоугольной системе координат определить, какая это линия.
Задание 7.
Даны два линейных преобразования:


Средствами матричного исчисления найти преобразование, выражающее x//1, x//2, x//3 через x1, x2, x3.
Задание 8.
Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей А.
А = 
Задание 9.
Найти пределы функции, не пользуясь правилом Лопиталя.
а) 
| в) 
|
б) 
| г) 
|
Задание 10.
Дано комплексное число z = 3 / ( 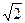 +i). Требуется 1) записать число z в алгебраической и тригонометрической формах; 2) найти все корни уравнения w3+z =0.
+i). Требуется 1) записать число z в алгебраической и тригонометрической формах; 2) найти все корни уравнения w3+z =0.
Вариант 16
Задание 1.
Дана система линейных уравнений

Доказать её совместность и решить двумя способами: 1) Методом Гаусса; 2) средствами матричного исчисления.
Задание 2.
Даны векторы a (5; 2; 1), b (8; -3; 2), c (-1; 2; 3), d (7; 9; 1) в некотором базисе. Показать, что векторы а, в, с образуют базис, и найти координаты вектора dв этом базисе.
Задание 3.
Даны координаты вершины пирамиды А1А2А3А4:A1 (5; -1; 3), A2 (8; 8; -3), A3 (2; 0; 2), A4 (4; 1; 0).
Найти:1)длину ребра А1А2; 2)угол между ребрами А1А2 И А1А4; 3)угол между ребром А1А4 и гранью А1А2А3; 4)площадь грани А1А2А3; 5)объем пирамиды; 6)уравнение прямой А1А2 ; 7)уравнение плоскости А1А2А3; 8)уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертеж.
Задание 4.
Даны стороны треугольника: x – y + 2 = 0 (AB), x = 2 (BC), x + y – 2 = 0 (AC). Составить уравнение прямо, проходящей через вершину В и через точку на стороне АС, делящую ее (считая от вершины А) в отношении 1:3. Сделать чертеж.
Задание 5.
Найти уравнение множества точек, равноотстоящих от окружности x2 + 4x + y2 = 0 и от точки М (2; 0).
Задание 6.
Линия задана уравнением в полярной системе координат 
Требуется:1)построить линию по точкам, начиная от 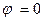 до
до  и придавая
и придавая 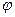 значения через промежуток
значения через промежуток 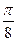 ; 2)найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3)по уравнению в декартовой прямоугольной системе координат определить, какая это линия.
; 2)найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3)по уравнению в декартовой прямоугольной системе координат определить, какая это линия.
Задание 7.
Даны два линейных преобразования:


Средствами матричного исчисления найти преобразование, выражающее x//1, x//2, x//3 через x1, x2, x3.
Задание 8.
Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей А.
А = 
Задание 9.
Найти пределы функции, не пользуясь правилом Лопиталя.
а) 
| в) 
|
б) 
| г) 
|
Задание 10.
Дано комплексное число z = 3 / ( 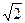 - I). Требуется 1) записать число z в алгебраической и тригонометрической формах; 2) найти все корни уравнения w3+z =0.
- I). Требуется 1) записать число z в алгебраической и тригонометрической формах; 2) найти все корни уравнения w3+z =0.
Вариант 17
Задание 1.
Дана система линейных уравнений

Доказать её совместность и решить двумя способами: 1) Методом Гаусса; 2) средствами матричного исчисления.
Задание 2.
Даны векторы a (1; 2; 3), b (-2; 3; -2), c (3; -4; -5), d (6; 20; 6) в некотором базисе. Показать, что векторы а, в, с образуют базис, и найти координаты вектора dв этом базисе.
Задание 3.
Даны координаты вершины пирамиды А1А2А3А4: A1 (6; 1; 1), A2 (4; 6; 6), A3 (4; 2; 0), A4 (1; 2; 6).
Найти:1)длину ребра А1А2; 2)угол между ребрами А1А2 И А1А4; 3)угол между ребром А1А4 и гранью А1А2А3; 4)площадь грани А1А2А3; 5)объем пирамиды; 6)уравнение прямой А1А2 ; 7)уравнение плоскости А1А2А3; 8)уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертеж.
Задание 4.
Найти уравнение прямой, проходящей через точку (-1; 1) так чтобы середина ее отрезка между прямыми x + 2y – 1 = 0 и x + 2y – 3 = 0 лежала на прямой x – y – 1 = 0. Сделать чертеж.
Задание 5.
Составить уравнение множества точек, расстояния которых от точки А (0; 1) в два раза меньше расстояния до прямой у – 4 = 0.
Задание 6.
Линия задана уравнением в полярной системе координат 
Требуется:1)построить линию по точкам, начиная от 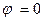 до
до  и придавая
и придавая 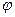 значения через промежуток
значения через промежуток 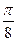 ; 2)найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3)по уравнению в декартовой прямоугольной системе координат определить, какая это линия.
; 2)найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3)по уравнению в декартовой прямоугольной системе координат определить, какая это линия.
Задание 7.
Даны два линейных преобразования:


Средствами матричного исчисления найти преобразование, выражающее x//1, x//2, x//3 через x1, x2, x3.
Задание 8.
Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей А.
А = 
Задание 9.
Найти пределы функции, не пользуясь правилом Лопиталя.
а) 
| в) 
|
б) 
| г) 
|
Задание 10.
Дано комплексное число z = 6 / (  +i). Требуется 1) записать число z в алгебраической и тригонометрической формах; 2) найти все корни уравнения w3+z =0.
+i). Требуется 1) записать число z в алгебраической и тригонометрической формах; 2) найти все корни уравнения w3+z =0.
Вариант 18
Задание 1.
Дана система линейных уравнений

Доказать её совместность и решить двумя способами: 1) Методом Гаусса; 2) средствами матричного исчисления.
Задание 2.
Даны векторы a (4; 2; 5), b (-3; 5; 6), c (2; -3; -2), d (8; 11; 13) в некотором базисе. Показать, что векторы а, в, с образуют базис, и найти координаты вектора dв этом базисе.
Задание 3.
Даны координаты вершины пирамиды А1А2А3А4:A1 (3; 3; 4), A2 (6; 9; 1), A3 (1; 7; 3), A4 (8; 5; 8).
Найти:1)длину ребра А1А2; 2)угол между ребрами А1А2 И А1А4; 3)угол между ребром А1А4 и гранью А1А2А3; 4)площадь грани А1А2А3; 5)объем пирамиды; 6)уравнение прямой А1А2; 7)уравнение плоскости А1А2А3; 8)уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертеж.
Задание 4.
В треугольнике АВС даны: уравнение стороны АВ 3x + 2y = 12, уравнение высоты ВМ x +2y = 4, уравнение высоты АМ 4x + y = 6, где М – точка пересечения высот. Написать уравнения сторон АС, ВС и высоты СМ. Сделать чертеж.
Задание 5.
Дана окружность x2 + y2 =4. Из точки А (-2; 0) проведена хорда АВ, которая продолжена на расстояние |ВМ| = |АВ|. Найти множество точек М.
Задание 6.
Линия задана уравнением в полярной системе координат 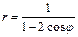
Требуется:1)построить линию по точкам, начиная от  до
до  и придавая
и придавая  значения через промежуток
значения через промежуток  ; 2)найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3)по уравнению в декартовой прямоугольной системе координат определить, какая это линия.
; 2)найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3)по уравнению в декартовой прямоугольной системе координат определить, какая это линия.
Задание 7.
Даны два линейных преобразования:


Средствами матричного исчисления найти преобразование, выражающее x//1, x//2, x//3 через x1, x2, x3.
Задание 8.
Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей А.
А = 
Задание 9.
Найти пределы функции, не пользуясь правилом Лопиталя.
а) 
| в) 
|
б) 
| г) 
|
Задание 10.
Дано комплексное число z = -6 / (  +i). Требуется 1) записать число z в алгебраической и тригонометрической формах; 2) найти все корни уравнения w3+z =0.
+i). Требуется 1) записать число z в алгебраической и тригонометрической формах; 2) найти все корни уравнения w3+z =0.
Вариант 19
Задание 1.
Дана система линейных уравнений
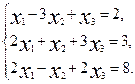
Доказать её совместность и решить двумя способами: 1) Методом Гаусса; 2) средствами матричного исчисления.
Задание 2.
Даны векторы a (1; 3; 2), b (-2; 3; -2), c (3; -4; -5), d (6; 20; 6) в некотором базисе. Показать, что векторы а, в, с образуют базис, и найти координаты вектора dв этом базисе.
Задание 3.
Даны координаты вершины пирамиды А1А2А3А4 :A1 (7; 2; 2), A2 (5; 7; 7), A3 (5; 3; 1), A4 (2; 3; 7).
Найти:1)длину ребра А1А2; 2)угол между ребрами А1А2 И А1А4; 3)угол между ребром А1А4 и гранью А1А2А3; 4)площадь грани А1А2А3; 5)объем пирамиды; 6)уравнение прямой А1А2; 7)уравнение плоскости А1А2А3; 8)уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертеж.
Задание 4.
Две стороны параллелограмма заданы уравнениями у = x – 2 и 5у = x + 6. Диагонали его пересекаются в начале координат. Написать уравнения двух других сторон параллелограмма и его диагоналей. Сделать чертеж.
Задание 5.
Составить уравнение линии, для каждой точки которой отношение расстояния от точки F (2; 0) к расстоянию до прямой x = 3 равно  . Сделать чертеж.
. Сделать чертеж.
Задание 6.
Линия задана уравнением в полярной системе координат 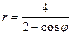
Требуется:1)построить линию по точкам, начиная от  до
до  и придавая
и придавая  значения через промежуток
значения через промежуток  ; 2)найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3)по уравнению в декартовой прямоугольной системе координат определить, какая это линия.
; 2)найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3)по уравнению в декартовой прямоугольной системе координат определить, какая это линия.
Задание 7.
Даны два линейных преобразования:


Средствами матричного исчисления найти преобразование, выражающее x//1, x//2, x//3 через x1, x2, x3.
Задание 8.
Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей А.
А = 
Задание 9.
Найти пределы функции, не пользуясь правилом Лопиталя.
а) 
| в) 
|
б) 
| г) 
|
Задание 10.
Дано комплексное число z = -1 / (i+  ). Требуется 1) записать число z в алгебраической и тригонометрической формах; 2) найти все корни уравнения w3+z =0.
). Требуется 1) записать число z в алгебраической и тригонометрической формах; 2) найти все корни уравнения w3+z =0.
Вариант 20
Задание 1.
Дана система линейных уравнений

Доказать её совместность и решить двумя способами: 1) Методом Гаусса; 2) средствами матричного исчисления.
Задание 2.
Даны векторы a (1; 3; 2), b (3; -1; 5), c (-6; 5; -3), d (12; -10; 6) внекотором базисе. Показать, что векторы а, в, с образуют базис, и найти координаты вектора dв этом базисе.
Задание 3.
Даны координаты вершины пирамиды А1А2А3А4 :A1 (1; 8; 2), A2 (5; 2; 6), A3 (5; 7; 4), A4 (4; 10; 9).
Найти:1)длину ребра А1А2; 2)угол между ребрами А1А2 И А1А4; 3)угол между ребром А1А4 и гранью А1А2А3; 4)площадь грани А1А2А3; 5)объем пирамиды; 6)уравнение прямой А1А2 ; 7)уравнение плоскости А1А2А3; 8)уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертеж.
Задание 4.
Написать уравнения сторон треугольника, зная одну его вершину А (0; 2) и уравнения высот ВМ x + y = 4 и СМ y = 2x, М – точка пересечения высот. Сделать чертеж.
Задание 5.
Составить уравнение линии, для каждой точки которой расстояние до начала координат и до точки А (0; 5) относятся как 3:2. Сделать чертеж.
Задание 6.
Линия задана уравнением в полярной системе координат 
Требуется:1)построить линию по точкам, начиная от  до
до  и придавая
и придавая  значения через промежуток
значения через промежуток  ; 2)найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3)по уравнению в декартовой прямоугольной системе координат определить, какая это линия.
; 2)найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3)по уравнению в декартовой прямоугольной системе координат определить, какая это линия.
Задание 7.
Даны два линейных преобразования:


Средствами матричного исчисления найти преобразование, выражающее x//1, x//2, x//3 через x1, x2, x3.
Задание 8.
Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей А.
А = 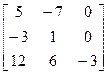
Задание 9.
Найти пределы функции, не пользуясь правилом Лопиталя.
а) 
| в) 
|
б) 
| г) 
|
Задание 10.
Дано комплексное число z =  / (1-i
/ (1-i  ). Требуется 1) записать число z в алгебраической и тригонометрической формах; 2) найти все корни уравнения w3+z =0.
). Требуется 1) записать число z в алгебраической и тригонометрической формах; 2) найти все корни уравнения w3+z =0.
Вариант 21
Задание 1.
Дана система линейных уравнений

Доказать её совместность и решить двумя способами: 1) Методом Гаусса; 2) средствами матричного исчисления.
Задание 2.
Даны векторы a(3,-2,1), b(-1,1,-2), c(2,1,-3), и d(11,-6,5).в некотором базисе. Показать, что векторы а, в, с образуют базис, и найти координаты вектора dв этом базисе.
Задание 3.
Даны координаты вершины пирамиды А1А2А3А4:
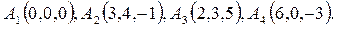
Найти:1)длину ребра А1А2; 2)угол между ребрами А1А2 И А1А4; 3)угол между ребром А1А4 и гранью А1А2А3; 4)площадь грани А1А2А3; 5)объем пирамиды; 6)уравнение прямой А1А2 ; 7)уравнение плоскости А1А2А3; 8)уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертеж.
Задание 4.
Составить уравнения прямых проходящих через вершины треугольника А(5;-4), В(-1;3), С(-3,-2) параллельно противоположным сторонам. Сделать чертеж.
Задание 5.
Написать уравнение траектории точки М(x; y),которая при своем движении остается втрое дальше от точки А(0;9), чем от точки В(0;2). Сделать чертеж.
Задание 6.
Линия задана уравнением в полярной системе координат 
Требуется:1)построить линию по точкам, начиная от  до
до  и придавая
и придавая  значения через промежуток
значения через промежуток  ; 2)найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3)по уравнению в декартовой прямоугольной системе координат определить, какая это линия.
; 2)найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3)по уравнению в декартовой прямоугольной системе координат определить, какая это линия.
Дата добавления: 2014-12-30; просмотров: 480; Мы поможем в написании вашей работы!; Нарушение авторских прав |