
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Непрерывные стохастические модели (Q-схемы)
4.1 Для каждого из приведенных условий подберите примеры, иллюстрирующие характер функционирования системы массового обслуживания:
- требования поступают в обслуживающую систему по одному;
- требования поступают в обслуживающую систему пачками;
- порядок поступления требований в систему известен заранее;
- поступления требований в систему случайны;
- источник требований неограничен;
- источник требований имеет ограниченную мощность;
- в очередь становится каждое из поступивших требований;
- возможен отказ со стороны поступивших требований от присоединения к очереди;
- имеет место дисциплина очереди «первым пришел – первым обслуживаешься»;
- имеет место дисциплина очереди «последним пришел – первым обслуживаешься»;
- имеет место случайный порядок обслуживания;
- дисциплина очереди построена на определенной системе приоритетов;
- присоединившиеся к очереди требования не покидают систему до тех пор, пока их не обслужат;
- некоторые требования покидают систему, не дождавшись обслуживания из-за фактора времени;
- имеется единственная очередь;
- имеется несколько параллельных очередей;
- возможен переход из очереди в очередь;
- обслуживающие приборы функционируют параллельно;
- обслуживающие приборы расположены последовательно;
- скорость обслуживания не зависит от длины очереди;
- скорость обслуживания зависит от длины очереди.
4.2 Выбрать операционные характеристики, которые необходимо измерить количественно, для расчета основных параметров работы СМО и оценки эффективности соответствующей функциональной системы.
4.3Определить оптимальное число телефонных номеров фирмы при условии, что заявки на переговоры поступают с интенсивностью λ=90 заявок в час, а средняя продолжительность разговора по телефону tобс=2мин. Определить показатели сначала для n=1 (одноканальной СМО). Интенсивность потока обслуживания μ=1/tобс = 30 заявок/час. Интенсивность нагрузки ρ=λ/μ=3.
4.4На АЗС есть 3 колонки, около станции 3 места для ожидания. На станцию в среднем прибывают 2 машины/мин. Среднее время заправки 1 машины – 1мин. Определить вероятность отказа от обслуживания и среднюю длину очереди.
4.5В пункте химчистки 3 аппарата, интенсивность потока посетителей λ=6 ед/ч. Интенсивность обслуживания одним аппаратом μ=3ед/ч. Среднее количество требований покидающих очередь не дождавшихся обслуживания υ=1ед/ч. Найти абсолютную пропускную способность этого пункта.
4.6На стоянку с пассажирами через промежутки времени, описываемые экспоненциальным распределением, прибывают такси. Пассажиры также прибывают в соответствии с пуассоновским законом. Интенсивность прибытия такси – λ1, а интенсивность прибытия пассажиров – λ2. В начальный момент времени t=0 нет пассажиров и нет такси, а в момент времени t на стоянке Х пассажиров и Y такси. Случайная величина Z=X-Y определит среднее значение очереди. Необходимо определить среднее значение z1 случайной величины Z и дисперсию D(Z).
4.7Магазин имеет 4 кассы, обслуживающие все отделы. Время обслуживания каждой кассой описывается функцией распределения В(t)=1-e-μt. Разработайте модель СМО для случая, когда поток покупателей пуассоновский с параметром λ. Во сколько раз изменится среднее время ожидания при 3 и 2 работающих кассах. Чему равно среднее время ожидания ω1 в очереди перед кассами?
4.8На стол контролера поступает поток деталей, интервалы времени между моментами поступления которых описываются распределением А(t)= 1-е-λt. Деталь бракуется с вероятностью Р и удаляется. Найти математическую модель потока небракованных деталей.
4.9На вход распределительного устройства поступает поток деталей, описываемый законом Пуассона с параметром λ. Устройство распределяет детали в порядке их поступления по n+1 направлениям, так что деталь с номером i mod (n+1), будет отправлена по i-му направлению. Получить модели потоков, расходящихся по n+1 направлениям в виде функции распределений длин интервалов между деталями Аi (t).
4.10На вход одноканальной СМО, имеющей постоянное время обслуживания в=1/μ, поступает пуассоновский поток заявок с параметром λ. Определить модель в виде распределения периода занятости. Определить среднее время периода занятости π1.
4.11ЭВМ обслуживает запросы первого (старшего) и второго приоритетов. Потоки запросов каждого из приоритетов описываются законами Пуассона с параметрами λ1 и λ2 соответственно. Запросы обслуживаются в соответствии с экспоненциальными законами распределения времени обслуживания. Для заявок первого приоритета В1(t)=1-е-μt, для заявок второго приоритета В2(t)=1-e-μt. Определить модель в виде распределения периода занятости П(t) или его характеристической функции π(s). Найти среднее время периода занятости π1.
4.12На вход СМО поступает пуассоновский поток заявок с параметром λ. Время обслуживания в каждой заявки постоянно и равно в=1/μ. Найти математическую модель в виде функции распределения периода занятости П(t).
4.13На участок цеха, содержащий n станков, поступают детали. Поток деталей пуассоновский с параметром λ. Детали обрабатываются на станках независимо друг от друга. Время обработки на всех станках определяется одним экспоненциальным распределением с параметром μ. Разработать модель участка, позволяющую найти среднее число деталей mср, ожидающих обработки; вероятность р3 того, что все станки заняты; среднее время ожидания tож.
4.14Разработать модель в виде СМО автоматизированной телефонной станции, которая позволил бы оценить следующие показатели: р0 – вероятность того, что все линии будут свободны; ротк – вероятность того, что абоненту будет отказано в обслуживании; N3 – среднее число занятых линий связи; к3 – коэффициент загрузки линий связи; N0 - среднее число свободных линий связи; кn – коэффициент простоя линий. Станция имеет n=5 линий связи. Поток требований на ведение разговоров пуассоновский с параметром λ – два вызова в единицу времени. Продолжительность каждого разговора подчинена показательному закону распределения. Среднее время tобс. необходимое для ведения разговора, равно одной единицы времени.
4.15Специализированный пост диагностики представляет собой одноканальную СМО. Число стоянок для автомобилей, ожидающих проведения диагностики, ограниченно и равно 3. Если все стоянки заняты, то очередной автомобиль, прибывший на диагностику, в очередь на обслуживание не становится. Поток автомобилей, прибывающих на диагностику, распределен по закону Пуассона и имеет интенсивность λ = 0.85 (автомобиля в час). Время диагностики автомобиля распределено по показательному закону и в среднем составляет 1.05 час. Требуется определить вероятностные характеристики поста диагностики, работающего в стационарном режиме.
4.16 На вход системы передачи информации сообщения поступают группами. Число сообщений в группе постоянно и равно m = 3. Поток групп сообщений простейший с плотностью λ = 5. Время передачи описывается показательным законом с математическим ожиданием 0,2сек. Поступающие сообщения, застав все каналы передачи информации занятыми, теряются. Разработать модель в виде СМО, которая позволила бы определить: Ротк – вероятность потери информации, к3 - коэффициент загрузки системы, кn – коэффициент простоя каналов. Определить, сколько каналов должна иметь система, чтобы Ротк <=0,05. Найти для этого случая кn, к3.
4.17 Рассматривается работа электронной цифровой вычислительной машины (ЭЦВМ). Среднее время безотказной работы ЭЦВМ равно 1/λ; поток отказов ЭЦВМ – простейший с параметром λ. Если в машине происходит сбой, то она останавливается и непрерывность устраняется. Среднее время устранения неисправности равно 1/μ; поток восстановлений ЭЦВМ – простейший с параметром μ. Определить вероятность того, что ЭЦВМ в момент времени t будет работать, если она в момент времени t = 0 работала.
4.18Рассматривается n-канальная система массового обслуживания смешанного типа, на вход которой поступает простейший поток заявок с плотностью λ. Число мест в очереди m. Время ожидания заявки в очереди Тож распределено по показательному закону со средним значением tср ож = 1/υ. Время обслуживания показательное со средним значением tср об = 1/ μ. Определить вероятности состояний системы. Найти вероятность Робс того, что заявка будет обслужена.
4.19Рассматривается работа автозаправочной станции (АЗС), на которой имеется четыре заправочных колонки (n=4). Заправка одной машины длится в среднем 3 минуты. В среднем на АЗС каждую минуту прибывает машина, нуждающаяся в заправке бензином. Число мест в очереди практически неограниченно. Все машины, вставшие в очередь на заправку, «терпеливо» дожидаются своей очереди. Определить среднее время, проходящее с момента прибытия машины на заправку, до момента её заправки, а также другие характеристики работы АЗС: среднее число занятых мест kср, среднее число машин в очереди sср, среднее время простоя колонки между заправками.
4.20Рассматривается система массового обслуживания следующего типа. Имеется m источников заявок (например, станков, которые могут требовать ремонта); они обслуживаются n каналами (например, бригадой из n наладчиков). Каждый источник заявок порождает поток заявок с плотностью λ, но только пока он не обслуживается; на время обслуживания поток заявок прекращается (станок останавливается и новых неисправностей не возникает). Обслуживание одной заявки продолжается в среднем время tср об = 1/μ. Если заявка застает все каналы занятыми, она становится в очередь и ожидает неограниченное время. Определить вероятности состояний системы.
4.21Пусть имеется 2-канальная СМО с числом мест в очереди 3. Интенсивность входного потока заявок составляет 6 заявок в час. Среднее время обслуживания одной заявки равно 90 мин. Требуется проанализировать работу СМО.
4.22Рассматривается работа автоматической телефонной станции, рассчитанной на одновременное обслуживание 20 абонентов (двадцатиканальная СМО). Вызов на АТС поступает в среднем через 6 с. Каждый разговор длится в среднем 2 мин. Если абонент застает АТС занятой, то он получает отказ. Найти вероятность того, что абонент, вызывая АТС, не застанет ее занятой и найти следующие характеристики работы СМО: среднее число занятых каналов, вероятность занятости канала, среднее время простоя канала.
4.23С целью увеличения дальности беспосадочного полета производится дозаправка самолетов горючим в воздухе. В районе дозаправки постоянно дежурят 4 самолета–дозаправщика. Дозаправка в среднем длится 10 минут. Если все дозаправщики заняты, то самолет, нуждающийся в заправке, может ожидать, совершая полет в течение 20 минут в районе дозаправки. Если же при этом он так и не дождался дозаправки, то он совершает посадку на запасной аэродром. Интенсивность полетов такова, что в среднем в район дозаправки прибывает 24 самолета. Определить вероятность того, что самолет будет заправлен, среднее число занятых дозаправщиков, вероятность занятости произвольно выбранного дозаправщика, среднее время простоя дозаправщика, среднее время цикла работы дозаправщика.
4.24Группа из 10 рыболовных траулеров обслуживается одной плавучей базой, принимающей на переработку рыбу и обеспечивающей траулер необходимыми материалами. Среднее время плавания траулера равно 3 суткам, на базе есть причал и среднее время обслуживания траулера равно 8 часам. Определить среднюю длину очереди, среднее время простоя траулера, среднее время простоя базы, среднее время ожидания заявки в очереди.
4.25Группа из 10 рыболовных траулеров обслуживается одной плавучей базой, принимающей на переработку рыбу и обеспечивающей траулер необходимыми материалами. Среднее время плавания траулера равно 3 суткам, на базе есть 3 причала и среднее время обслуживания траулера равно 8/3 часа. Определить среднюю длину очереди, среднее время простоя траулера, среднее время простоя базы, среднее время ожидания заявки в очереди.
4.26Рассматривается работа столовой. Обеды выдают 4 человека. Количество мест для размещения людей, уже получивших обед, всегда достаточно. Среднее время выдачи обеда для одного посетителя равно 4 мин. Прибывает в среднем 2 человека в минуту, и в очереди могут одновременно находиться не более 20 человек. В среднем посетитель стоит в очереди 10 минут, после чего он покидает столовую. Определить вероятность того, что посетитель, направляющийся в столовую, пообедает, и выяснить, сколько на это ему понадобится времени, если на прием пищи в среднем затрачивается 10 мин. Определить количество столов, которое необходимо иметь в столовой, чтобы с вероятностью 0,95 посетитель, получивший обед, смог найти себе место, если у каждого стола есть 4 места для размещения посетителей столовой.
5Сетевые модели (N-схемы)
5.1. Пусть процесс функционирования некоторой реальной системы S (процессор ЭВМ, мультиплексный канал, станок в технологической цепочке и т. п.), являющийся по своей природе процессом обслуживания, представлен в виде двухфазной одноканальной Q- схемы:

Пусть имеется некоторая система S, например, производственно-технологическая, процесс функционирования которой представлен в виде Q-схемы:

По технологическому циклу для выполнения заказа необходимо выполнить две фазы обслуживания: сначала обслуживание в канале К1, затем либо в К2, либо в К3. Операторы F1 и F2 обслуживают (поддерживают в работоспособном состоянии) каналы, причем F1 обслуживает К, и К2, a F2 — K1 и К3. Тогда в этой системе могут быть следующие состояния:
а — заказ пришел и ждет в накопителе Н1;
б — заказ обработан К1, и ждет в накопителе Н2;
в— заказ выполнен и находится в накопителе Н3;
г — канал К1, не занят;
д — канал К2 не занят;
е — канал К3 не занят;
ж — оператор F1 не занят;
з — оператор F2 не занят;
и — канал К1, выполняет заказ под управлением F1;
к — канал К1, выполняет заказ под управлением F2;
л — канал К2 выполняет заказ под управлением F1
м — канал К3 выполняет заказ под управлением F2
и могут происходить следующие события-переходы:
1— поступление заказа;
2— F1 начинает выполнение заказа на К;
3— F1 закончил выполнение заказа на К;
4— F2 начинает выполнение заказа на К1;
5— F2 закончил выполнение заказа на К1;
6— F1 начинает выполнение заказа на К2;
7— F1 закончил выполнение заказа на К2;
8— F2 начинает выполнение заказа на К3;
9— F2 закончил выполнение заказа на К3;
10— заказ отправляется на доставку.
Формализовать процесс при помощи N-схемы, считая, что состояниям системы соответствуют позиции N-схемы, событиям — переходы. Нанести маркировку, соответствующую такому состоянию системы, при котором каналы свободны, операторы не заняты, в системе нет заказов.
5.2 Рассмотрим процесс функционирования ЭВМ с конвейерной обработкой. При построении высокопроизводительных асинхронных ЭВМ широко применяют метод конвейерной обработки чисел. Этот метод обработки подобен функционированию сборочного конвейера и особенно удобен для работы с век торами в массивами. Конвейер состоит из набора операций, которые могут выполняться одновременно в разных блоках ЭВМ. Когда операция в k-м блоке завершается, ее результат передается в (k+ 1)-й блок, a k-й блок принимает результат операции из (k - 1)-го блока. Если каждая операция запускается по завершении предыдущей, то имеем дело с асинхронным способом управления конвейером. Для управления k-м блоком такого конвейера необходима информация о выполнении следующих условий:
входной регистр заполнен;
входной регистр пуст;
выходной регистр заполнен;
выходной регистр пуст;
блок k занят;
блок k свободен;
пересылка осуществляется.
Формализовать процесс при помощи N-схемы, считая, что состояниям системы соответствуют позиции N-схемы, событиям — переходы. Нанести маркировку, соответствующую такому состоянию системы, при котором каналы свободны, операторы не заняты, в системе нет заказов.
5.3 Рассмотрим принципы программирования N-схем в языке MODAL, который предназначен для моделирования и реализации вычислительных алгоритмов на базе N-схем (сетей Петри). Он содержит семь операторов:
START — описание начальной маркировки;
STOP — описание конечной маркировки;
T(MOD) — описание структуры сети Петри;
 TYPE — оператор промежуточного вывода на печать;
TYPE — оператор промежуточного вывода на печать;
СOMMENT
COMPLEKXITY - вспомогательные операторы;
END — конец
Формализовать процесс при помощи N-схемы, считая, что состояниям системы соответствуют позиции N-схемы, событиям — переходы. Нанести маркировку, соответствующую такому состоянию системы, при котором каналы свободны, операторы не заняты, в системе нет заказов.
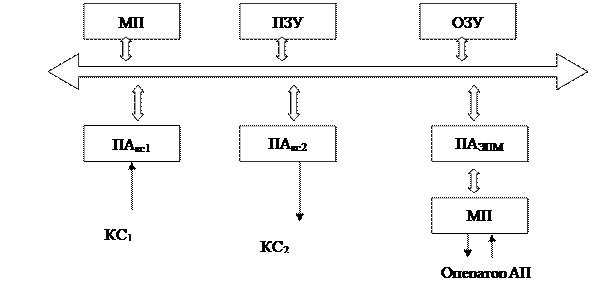
5.4 Построим в виде N-схемы модель микропроцессорного абонентского пункта (АП) информационно-вычислительной сети. Структура этого АП показана на рисунке, где обозначено: МП — микропроцессор; ОЗУ — оперативное запоминающее устройство; ПА — периферийный адаптер; ЭПМ — электрифицированная пишущая машинка; КС1 и КС2 — входной и выходной каналы связи. Задание Ns-схемы в виде временной сети включает в себя задание структуры <B, D, I, O>, вектора разметок М0 и вектора задержек Z.
Структуру Ns -схемы зададим графически, так как именно графическое представление обладает наибольшей наглядностью и простотой соотношения со структурой объекта, т. е. в данном примере со структурой АП. На рисунке для наглядности пунктиром выделены элементы Ns-схемы, относящиеся к конкретным элементам структуры АП.
Вектор разметок имеет вид М0 = (010100001110000001 Nb0), а вектор задержек
Z = (zBX, 0, zKC1, 0, 0, zлм1,0, zЛМ, 0, 0, 0, zВХ2, zПМ2, О, zКС1, 0,0).
Формализовать процесс при помощи N-схемы, считая, что состояниям системы соответствуют позиции N-схемы, событиям — переходы. Нанести маркировку, соответствующую такому состоянию системы, при котором каналы свободны, операторы не заняты, в системе нет заказов.
5.5 Поступление метки во входную позицию перехода dmинициирует процедуру проверки готовности перехода к срабатыванию. Проверяемые при этом условия включают в себя анализ разметки решающей позиции M{bk}, где  , а также проверку разметки выходных позиций M{О(dm)} и сопряженных позиций M{I(dm)}. В том случае, когда
, а также проверку разметки выходных позиций M{О(dm)} и сопряженных позиций M{I(dm)}. В том случае, когда  , на данной фазе производится также вычисление решающей процедуры перехода z (dm).
, на данной фазе производится также вычисление решающей процедуры перехода z (dm).
При достижении требуемых условий переход вступает в активную фазу, содержание которой определяется элементами описания перехода i(dm) и p(dm),причем элемент t(dm)может быть задан либо непосредственно, либо в виде функции. В последнем случае необходимо предварительно вычислить эту функцию, а затем моделировать требуемое время t (dm).
Процедура перехода p(dm)выполняется в два этапа: сначала вычисляются предикаты Пj, а затем реализуется требуемое подмножество операций над описателями меток {ljp }. Далее переход dm вступает в фазу завершения, содержанием которой является смена разметки входных и выходных позиций перехода М {I(dm)} и M(O(dm)}.Разметка позиции bi, меняется на нулевую: M(bi):=0. При  разметка решающей позиции становится неопределенной: M(bk):=e0. Затем выполняется перемещение меток в ряд выходных позиций O(dm)в соответствии с типом данного перехода. Эта операция завершает работу перехода по обработке поступившей метки.
разметка решающей позиции становится неопределенной: M(bk):=e0. Затем выполняется перемещение меток в ряд выходных позиций O(dm)в соответствии с типом данного перехода. Эта операция завершает работу перехода по обработке поступившей метки.
Формализовать процесс при помощи N-схемы, считая, что состояниям системы соответствуют позиции N-схемы, событиям — переходы. Нанести маркировку, соответствующую такому состоянию системы, при котором каналы свободны, операторы не заняты, в системе нет заказов.

5.6Проведем анализ соответствия между элементами NE - схем и объектами языка моделирования GPSS. В результате сравнительного анализа можно сформулировать следующее.
1. Метка NE-схемы может быть представлена динамическим объектом GPSS, т.е. транзактом.
2. Описатели меток аналогичны параметрам транзактов GPSS.
3. Позиция NE-схемы идентична объекту, принадлежащему к аппаратной категории GPSS типа накопителя единичной емкости.
4. Решающие позиции 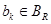 NE схемы в зависимости от принадлежности к множеству Вp реализуются двумя способами:
NE схемы в зависимости от принадлежности к множеству Вp реализуются двумя способами:
а) если  , то bk эквивалентна набору объектов типа булевых переменных вычислительной категории GPSS;
, то bk эквивалентна набору объектов типа булевых переменных вычислительной категории GPSS;
б) если  , то bk может быть представлена накопителем единичной емкости аппаратной категории GPSS.
, то bk может быть представлена накопителем единичной емкости аппаратной категории GPSS.
5. Временные параметры переходов I (dm) реализуются объектом ADVANCE операционной категории GPSS.
6. Операции вычисления предикатов Пj, 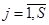 , для p(dm)соответствует применение блока TESTE, изменяющего маршруты транзактов, в сочетании с булевыми переменными вычислительной категории GPSS.
, для p(dm)соответствует применение блока TESTE, изменяющего маршруты транзактов, в сочетании с булевыми переменными вычислительной категории GPSS.
7. Операции {ljp}для p(dm)выполняются с помощью блоков ASSIGN динамической категории GPSS в сочетании с арифметическими переменными.
8. Хранение значений описателей меток можно имитировать путем записи значений параметров транзактов в ячейки хранимых значений (X, ХН) с помощью блока SAVEVALVE запоминающей категории GPSS.
9. Процессы синхронизации движения меток через переход dmи удаления меток из решающей позиции 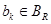 , могут быть обеспечены с помощью огических переключателей LOG IC S и LOGIC R аппаратной категории GPSS.
, могут быть обеспечены с помощью огических переключателей LOG IC S и LOGIC R аппаратной категории GPSS.
10. Макропозиция генератора аналогична блоку GENERATE динамической категории GPSS.
11. Макропозиция поглощения функционально идентичена блоку ERMINATE динамической категории GPSS.
12. Макропозиция очереди может интерпретироваться в GPSS записью транзакта в цепь пользователя.
Формализовать процесс при помощи N-схемы, считая, что состояниям системы соответствуют позиции N-схемы, событиям — переходы. Нанести маркировку, соответствующую такому состоянию системы, при котором каналы свободны, операторы не заняты, в системе нет заказов.
Модели календарного планирования
6.1. Компания с ограниченной ответственностью выполняет заказ. Проект содержит работы, информация по которым задана таблицей:
| Операция | Непосредственно предшествующие операции | Оптимистический прогноз времени выполнения, дней | Пессимистический прогноз времени выполнения, дней | Стоимость для ожидаемой продолжительности, ден. ед. |
| А В С D E F G H | - - - А В С D, Е G, F |
Сделайте анализ проекта, рассчитайте временные параметры при помощи сетевого графика. Каково наименьшее возможное время выполнения всего проекта? Какова минимальная стоимость завершения пректа к этому сроку?
6.2. Компания намерена учредить дочернюю фирму. Проект содержит работы, информация по которым задана таблицей:
| Операция | Непосредственно предшествующие операции | Стандартное время, дней |
| А В С D E F G H I J | - А А А В D D G С,Е, F G, I |
Сделайте анализ проекта, рассчитайте временные параметры при помощи сетевого графика. Каково наименьшее возможное время выполнения всего проекта?
6.3.В Институте подготовки специалистов по принятию решений действует ежегодная программа чтения лекций.
| Операция | Непосредственно предшествующие операции | Стандартное время, дней | Критическое время, дней | Дополнительные издержки, ден. ед. |
| А Выбор дат проведения лекций В Назначение лекторов и согласование лекционных тем С Подготовка рекламных материалов D Обновление списка студентов заочной формы обучения E Подготовка списков оплаты сотрудникам F Корректировка списков и программ G Распечатка материалов H Брошюровка материалов I Рассылка материалов J Проведение собеседований | - A - - D B,C,E F G E H,I | - |
Сделайте анализ проекта, рассчитайте временные параметры при помощи сетевого графика. Каково наименьшее возможное время выполнения всего проекта? Какова минимальная дополнительная стоимость завершения пректа к этому сроку
6.4. Компания намерена реализовать проект, содержащий работы, информация по которым задана таблицей:
| Операция | Непосредственно предшествующие операции | Стандартное время, дней |
| А В С D E F G H I J | - А А В D В С F, G Е, Н I | Не определено Не определено |
Если необходимо выполнить проект не более, чем за 19 дней, какие ограничения необходимы для сроков выполнения работ F и Н?
После дополнительных исследований, стало известно, что t(F)=2, t(Н)=1, а неопределенность этих значений распределено по закону Пуассона. Найти вероятность того, проект можно выполнить не более, чем за 19 дней.
6.5. Компания с ограниченной ответственностью выполняет заказ. Проект содержит работы, информация по которым задана таблицей:
| Операция | Непосредственно предшествующие операции | Ожидаемое время выполнения, недель | Потребность в персонале |
| А Первичные разработки В Исследование рынка С Получение технических стандартов D Создание образца E Подготовка рыночной базы F Расчёт стоимости G Испытание продукта H Выборочный контроль I Предварительная оценка значения цены J Итоговый отчет | - - А А А С D В,Е H G, F, I |
Сделайте анализ проекта, рассчитайте временные параметры при помощи сетевого графика. Каково наименьшее возможное время выполнения всего проекта? При помощи графика Ганта выяснить потребность в персонале на любой момент времени. Как следует распределить персонал, чтобы выполнить проект за наименее возможный срок с наименьшим количеством исполнителей? Достаточно ли 9 человек для выполнения проекта за наименее возможный срок?
6.6Процесс составления бюджета разделяется на следующие этапы:
| Операция | Непосредственно предшествующие операции | Стандартное время, дней |
| А Оценка ставок заработной платы В Разработка прогнозов рынка С Определение цен продаж D Составление бюджета для объёмов продаж E Составление бюджета доходов от продажи F Составление бюджета расходов по продаже G Составление бюджета объёмов производства H Составление бюджета накладных расходов I Составление бюджета трудовых ресурсов J Составление бюджета сырья К Составление бюджета производственных площадей и оборудования L Выработка прогноза общей прибыли | - - - В С, D А, D D А А, G G G Е, F, Н, I, J ,К |
Можно ли закончить данный проект за 17 недель?
6.7 Процесс внедрения в производство нового вида продукции разделяется на следующие этапы:
| Операция | Непосредственно предшествующие операции | Стандартное время, дней |
| А Создание новой продукции В Создание упаковки С Подготовка производственных мощностей D Получение сырья и материалов E Выпуск опытной партии продукции F Упаковка продукции G Принятие решения о выборе пробного рынка сбыта H Упаковка опытной партии I Поставка продукции на пробный рынок сбыта J Реализация продукции на пробном рынке сбыта К Оценка результатов внедрения продукции на рынок L Планирование выпуска продукции на общем уровне | - - А А С, D В - Е, F Н, G I J К |
Сделать анализ временных параметров проекта.
Время некоторых операций подвержено влиянию случайных факторов
| Операция | Оптимистический прогноз времени выполнения, недель | Пессимистический прогноз времени выполнения, недель |
| А В D К L |
Определите ожидаемое время выполнения всего проекта, и оцените вероятность того, что оно превысит 35 недель.
Дата добавления: 2015-01-05; просмотров: 325; Мы поможем в написании вашей работы!; Нарушение авторских прав |