
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Ранг матрицы
Рассмотрим матрицу А размера m × n.

 .
.
 Выделим в ней k строк и k столбцов (k ≤ min(m;n)). Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k-го порядка. Все такие определители называются минорами этой матрицы. В матрице А пунктиром выделен минор 2-го порядка. (Заметим, что таких миноров можно составить
Выделим в ней k строк и k столбцов (k ≤ min(m;n)). Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k-го порядка. Все такие определители называются минорами этой матрицы. В матрице А пунктиром выделен минор 2-го порядка. (Заметим, что таких миноров можно составить 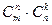 штук, где
штук, где  – число сочетаний из n элементов по k.)
– число сочетаний из n элементов по k.)
Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рантом матрицы. Обозначается r, r(A) или rang A.
 Очевидно, что
Очевидно, что  , где
, где  – меньшее из чисел m и n.
– меньшее из чисел m и n.
Минор, порядок которого определяет ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров.

Пример 3.4. Найти ранг матрицы:


 Решение: Все миноры 3-го порядка равны нулю. Есть минор 2-го порядка, отличный от нуля
Решение: Все миноры 3-го порядка равны нулю. Есть минор 2-го порядка, отличный от нуля  . Значит,
. Значит, 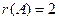 . Базисный минор стоит на пересечении 2 и 3 строки с 1 и 3 столбцами.
. Базисный минор стоит на пересечении 2 и 3 строки с 1 и 3 столбцами.
Отметим свойства ранга матрицы:
1. При транспонировании матрицы ее ранг не меняется.
2. Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится.
3. Ранг матрицы не изменится при элементарных преобразованиях матрицы (см. с. 3).
Ранг канонической матрицы равен числу единиц на главной диагонали. На этом основан один из способов вычисления ранга матрицы.

Пример 3.5. Найти ранг матрицы

используя результаты примера 1.4.
 Решение: В примере 1.4. показано, что
Решение: В примере 1.4. показано, что
 ~
~  ,
,
то есть
 ~
~  .
.
 Таким образом, ранг матрицы А равен
Таким образом, ранг матрицы А равен 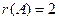 .
.
Дата добавления: 2015-01-15; просмотров: 257; Мы поможем в написании вашей работы!; Нарушение авторских прав |