Произведение матриц

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.

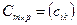Произведением матрицы на матрицу называется матрица такая, что

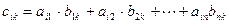, где ,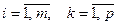

т.е. элемент i-ой строки и k-го столбца матрицы произведения C равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы k-го столбца матрицы В.

Получение элемента схематически изображается так:

.

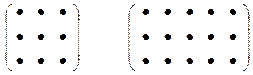Если матрицы А и В квадратные одного размера, то произведение А В и В А всегда существует. Легко показать, что А · Е = Е · А = А, где А – квадратная матрица, Е – единичная матрица того же размера.

Пример 1.5. .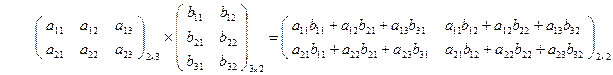

Пример 1.6. 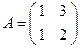, . Тогда произведение А · В не определено, так как число столбцов матрицы А (3) не совпадает с числом строк матрицы В (2). При этом определено произведение В × А, которое считают следующим образом:

.

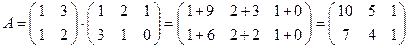Матрицы А и В называются перестановочными, если АВ = ВА.

Умножение матриц обладает следующими свойствами:

1. А · (В · С) = (А · В) · С;
2. А · (В + С) = АВ + ВС;

3. (А + В) · С = АС + ВС;

4. α(АВ) = (αА)В.

если, конечно, написанные суммы и произведения матриц имеют смысл.

Для операции транспонирования верны свойства:

1. (А + В)^Т = А^Т + В^Т;
2. (АВ)^Т = В^Т + А^Т.